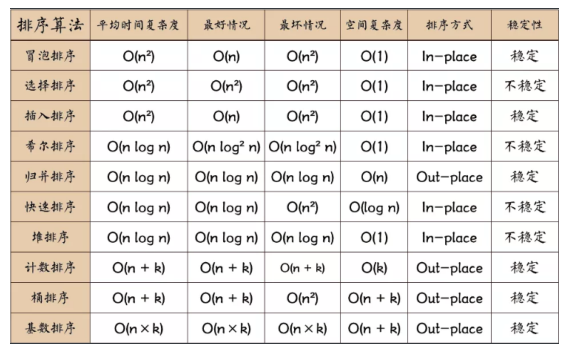
87、十大排序算法及其时间和空间复杂度

（1）冒泡排序

算法描述： ⽐较相邻的元素。如果第⼀个⽐第⼆个⼤，就交换它们两个； 对每⼀对相邻元素作同样的⼯作，从开始第⼀对到结尾的最后⼀对，这样在最后的元素应 该会是最⼤的数； 针对所有的元素重复以上的步骤，除了最后⼀个； 重复步骤 1~3，直到排序完成。 ⽤⼀个例⼦，带你看下冒泡排序的整个过。我们要对⼀组数据 4，5，6，3，2，1，从⼩到 到⼤进⾏排序。第⼀次冒泡操作的详细过程就是这样

可以看出，经过⼀次冒泡操作之后，6 这个元素已经存储在正确的位置上。要想完成所有数据 的排序，我们只要进⾏ 6 次这样的冒泡操作就⾏了。

下⾯代码中 std::swap 函数的源代码如下，可以看到有三个赋值操作：

template<class T>
void swap(T &a, T &b) {
 T temp = a;
 a = b;
 b = temp;
}
void BubbleSort(std::vector<int> &nums, int n) {
 if (n <= 1) return;
 bool is_swap;
 for (int i = 1; i < n; ++i) {
 is_swap = false;
 //设定⼀个标记，若为false，则表示此次循环没有进⾏交换，也就是待排序列已经有
序，排序已经完成。
 for (int j = 1; j < n - i + 1; ++j) {
 if (nums[j] < nums[j-1]) {
 std::swap(nums[j], nums[j-1]);
 is_swap = true;//表示有数据交换
 }
 }
 if (!is_swap) break;//没有数据交集，提前退出
}
}
int main() {
 int a[] = {34,66,2,5,95,4,46,27};
 BubbleSort(a,sizeof(a)/sizeof(int)); //cout => 2 4 5 27 34 46 66 95
 return 0;
}

（2）插⼊排序

算法描述：分为已排序和未排序 初始已排序区间只有⼀个元素 就是数组第⼀个 遍历未排序的 每⼀个元素在已排序区间⾥找到合适的位置插⼊并保证数据⼀直有序。

void InsertSort(std::vector<int> &nums,int n) {
 if (n <= 1) return;
 for(int i = 0; i < n; ++i) {
 for (int j = i; j > 0 && nums[j] < nums [j-1]; --j) {
 std::swap(nums[j],nums[j-1]);
 }
 }
}
int main() {
 std::vector<int> nums = {4,6,5,3,2,1};
 InsertSort(nums,6);//cout => 1,2,3,4,5,6
 return 0;
}

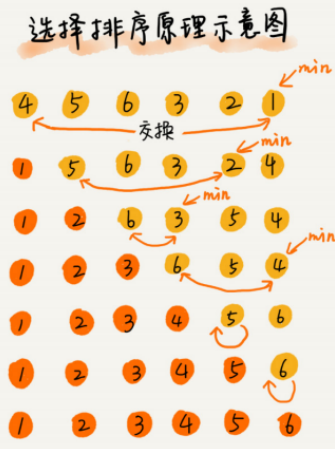
（3）选择排序

算法描述：分已排序区间和未排序区间。每次会从未排序区间中找到最⼩的元素，将其放到已排序区间的末尾。

void SelectSort(std::vector<int> &nums, int n) {
 if (n <= 1) return;
 int mid;
 for (int i = 0; i < n - 1; ++i) {
 mid = i;
 for (int j = i + 1; j < n; ++j) {
 if (nums[j] < nums[mid]) {
 mid = j;
 }
 }
 std::swap(nums[mid],nums[i]);
 }
}

【时间 ,空间复杂度/是否稳定？】

⾸先，选择排序空间复杂度为 O(1)，是⼀种原地排序算法。选择排序的最好情况时间复杂度、最坏情况和平均情况时间复杂度都为O(n)。你可以⾃⼰来分析看看。

那选择排序是稳定的排序算法吗？答案是否定的，选择排序是⼀种不稳定的排序算法。从图中，你可以看出来，选择排序每次都要找剩余未排序元素中的最⼩值，并和前⾯的元素交换位 置，这样破坏了稳定性。 【思考】冒泡排序和插⼊排序的时间复杂度都是 O(n)，都是原地排序算法，为什么插⼊排序 要⽐冒泡排序更受欢迎呢？

【思路】冒泡排序不管怎么优化，元素交换的次数是⼀个固定值，是原始数据的逆序度。插⼊ 排序是同样的，不管怎么优化，元素移动的次数也等于原始数据的逆序度。但是，从代码实现 上来看，冒泡排序的数据交换要⽐插⼊排序的数据移动要复杂，冒泡排序需要 3 个赋值操作，⽽插⼊排序只需要 1 个。把执⾏⼀个赋值语句的时间粗略地计为单位时间，处理相同规模的数，插⼊排序⽐冒泡排序减少三倍的单位时间！

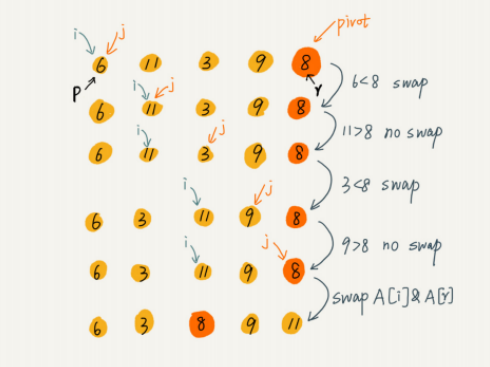
（4）快排

算法描述：先找到⼀个枢纽；在原来的元素⾥根据这个枢纽划分 ⽐这个枢纽⼩的元素排前 ⾯；⽐这个枢纽⼤的元素排后⾯；两部分数据依次递归排序下去直到最终有序。

void QuickSort(std::vector<int> &nums,int l,int r) {
 if (l + 1 >= r) return;
 int first = l, last = r - 1 ,key = nums[first];
 while (first < last) {
 while (first < last && nums[last] >= key) last--;//右指针 从右向左
扫描 将⼩于piv的放到左边
 nums[first] = nums[last];
 while (first < last && nums[first] <= key) first++;//左指针 从左向
右扫描 将⼤于piv的放到右边
 nums[last] = nums[first];
 }
 nums[first] = key;//更新piv
 quick_sort(nums, l, first);//递归排序 //以L为中间值，分左右两部分递归调⽤
 quick_sort(nums, first + 1, r);
}
int main() {
 int a[] = {0,34,66,2,5,95,4,46,27};
 QuickSort(a, 0, sizeof(a)/sizeof(int));
 for(int i=0; i<=8; ++i) {
 std::cout<<a[i]<<" "; // print => 0 2 4 5 27 34 46 66 95
 }
 std::cout<<endl;
 return 0;
}

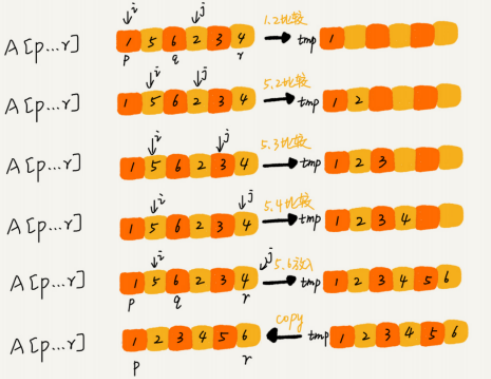
（5）归并排序

算法描述：归并排序是⼀个稳定的排序算法，归并排序的时间复杂度任何情况下都是O(nlogn)，归并排序不是原地排序算法⽤两个游标 i 和j，分别指向 A[p…q] 和A[q+1…r] 的第⼀个元素。⽐较这两个元素 A[i] 和 A[j]，如果 A[i]<=A[j]，我们就把 A[i] 放⼊到临时数组 tmp，并且 i 后移⼀位，否则将 A[j] 放⼊ 到数组 tmp， j 后移⼀位。

void mergeCount(int a[],int L,int mid,int R) {
 int *tmp = new int[L+mid+R];
 int i=L;
 int j=mid+1;
 int k=0;
 while( i<=mid && j<=R ) {
 if(a[i] < a[j])
 tmp[k++] = a[i++];
 else
 tmp[k++] = a[j++];
 }
 ///判断哪个⼦数组中有剩余的数据
 while( i<=mid )
 tmp[k++] = a[i++];
 while( j<=R)
 tmp[k++] = a[j++];
 /// 将 tmp 中的数组拷⻉回 A[p...r]
 for(int p=0; p<k; ++p)
 a[L+p] = tmp[p];
 delete tmp;
}
void mergeSort(int a[],int L,int R) {
 ///递归终⽌条件 分治递归
 /// 将 A[L...m] 和 A[m+1...R] 合并为 A[L...R]
 if( L>=R ) { return; }
 int mid = L + (R - L)/2;
 mergeSort(a,L,mid);
 mergeSort(a,mid+1,R);
 mergeCount(a,L,mid,R);
}
int main() {
 int a[] = {0,34,66,2,5,95,4,46,27};
 mergeSort(a, 0, sizeof(a)/sizeof(int));
 for(int i=0; i<=8; ++i) {
 std::cout<<a[i]<<" "; // print => 0 2 4 5 27 34 46 66 95
 }
 std::cout<<endl;
 return 0;
}

（6）堆排序

算法描述：利⽤堆这种数据结构所设计的⼀种排序算法。堆积是⼀个近似完全⼆叉树的结构， 并同时满⾜堆积的性质：即⼦结点的键值或索引总是⼩于（或者⼤于）它的⽗节点。堆排序可 以⽤到上⼀次的排序结果，所以不像其他⼀般的排序⽅法⼀样，每次都要进⾏ n-1 次的⽐较， 复杂度为O(nlogn) 。

算法步骤：

1、利⽤给定数组创建⼀个堆 H[0..n-1] （我们这⾥使⽤最⼩堆），输出堆顶元素

2、以最后⼀个元素代替堆顶，调整成堆，输出堆顶元素

3、把堆的尺⼨缩⼩ 1

4、重复步骤 2，直到堆的尺⼨为 1

建堆：将数组原地建成⼀个堆，不借助额外的空间，采⽤从上往下的堆化（对于完全⼆叉树来 说，下标是 n/2+1 到 n 的节点都是叶⼦节点，不需要堆化）。

排序： ”删除堆顶元素“：当堆顶元素移除之后，把下标为 n 的元素放到堆顶，然后在通过堆化 的⽅法，将剩下的 n - 1 个元重新构建成堆，堆化完成之后，在取堆顶的元素，放到下标为 n-1 的位置，一直重复这个过程，直到最后堆中只剩下标 1 的⼀个元素。

/*
优点：O(nlogn)，原地排序，最⼤的特点：每个节点的值⼤于等于(或⼩于等于)其⼦树节点
（7）桶排序
算法描述：将数组分到有限数ᰁ的桶⾥。每个桶再个别排序（有可能再使⽤别的排序算法或是
以递归⽅式继续使⽤桶排序进⾏排序）。
缺点：相⽐于快排，堆排序数据访问的⽅式没有快排友好；数据的交换次数要多于快排。
*/
void HeapSort(int a[], int n) {
 for(int i=n/2; i>=1; --i) {
 Heapify(a, n, i);
 }
 int k = n;
 while( k > 1) {
 swap(a[1],a[k]);
 --k;
 Heapify(a,k,1);
 }
}
void Heapify(int a[], int n, int i) {
 while (1) {
 int maxPos = i;
 if (i*2 <= n && a[i] < a[i*2]) { maxPos = i*2; }
 if (i*2+1 <= n && a[maxPos] < a[i*2+1]) { maxPos = i*2+1; }
 if (maxPos == i) break;
 std::swap(a[i], a[maxPos]);
 i = maxPos;
 }
}
void

（8）计数排序

扩展：如果在⾯试中有⾯试官要求你写⼀个 O(n) 时间复杂度的排序算法，可不要傻乎乎的说这不可能！虽然前⾯基于⽐较的排序的下限是O(nlogn)。但是确实也有线性时间复杂度的排序，只不过有前提条件，就是待排序的数要满⾜⼀定的范围的整数，⽽且计数排序需要⽐较多的辅助空间。

算法描述：其基本思想是，⽤待排序的数作为计数数组的下标，统计每个数字的个数。然后依 次输出即可得到有序序列。 假设有 8 个考⽣，分数在 0 到 5 分之间。这 8 个考⽣的成绩我们放在⼀个数组 A[8]中，它们分别是： 2， 5， 3， 0， 2， 3， 0， 3 。

考⽣的成绩从 0 到 5 分，我们使⽤⼤⼩为 6 的数组 C[6]表示桶，其中下标对应分数。不过，C[6]内存储的并不是考⽣，⽽是对应的考⽣个数。像我刚刚举的那个例⼦，我们只需要遍历⼀ 遍考⽣分数，就可以得到 C[6]的值。

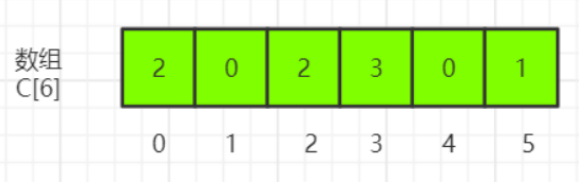
这是我们的数组，从图中可以看出，分数为 3 分的考⽣有 3 个，⼩于 3 分的考⽣有 4 个，所 以，成绩为 3 分的考⽣在排序之后的有序数组 R[8]中，会保存下标 4， 5， 6 的位置。

那我们如何快速计算出，每个分数的考⽣在有序数组中对应的存储位置呢？

我们对 C[6] 数组顺序求和， C[6]存储的数据就变成了下⾯这样⼦。 C[k]⾥存储小于等于分数 k的考⽣个数。

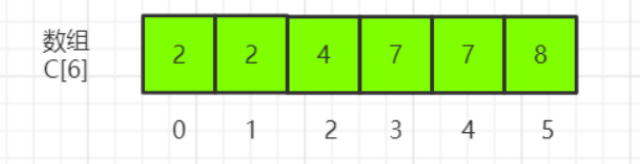
我们从后到前依次扫描数组 A。⽐如，当扫描到 3 时，我们可以从数组 C 中取出下标为 3 的值 7，也就是说，到目前为止，包括⾃⼰在内，分数⼩于等于 3 的考⽣有 7 个，也就是说 3 是数组 R 中的第 7 个元素（也就是数组 R 中下标为 6 的位置）。当 3 放⼊到数组 R 中后，小于等于 3 的元素就只剩下了 6 个了，所以相应的 C[3]要减 1，变成 6。

以此类推，当我们扫描到第 2 个分数为 3 的考⽣的时候，就会把它放⼊数组 R 中的第 6 个元 素的位置（也就是下标为 5 的位置）。当我们扫描完整个数组 A 后，数组 R 内的数据就是按 照分数从⼩到⼤有序排列的了。 注意：计数排序只能⽤在数据范围不⼤的场景中，如果数据范围 k ⽐要排序的数据 n ⼤很多，就不适合⽤计数排序了。⽽且，计数排序只能给⾮负整数排序，如果要排序的数据是其他 类型的，要将其在不改变相对⼤⼩的情况下，转化为⾮负整数。

void countSort(int *a,int n){
 int maxV=a[0];
 for(int i=1; i<n; ++i){
 maxV=max(maxV,a[i]);
 }
 int c[maxn];
 memset(c,0,sizeof(c));
 for(int i=0; i<n; ++i){
        c[a[i]]++;
 }
 for(int i=1; i<=maxV; ++i){
 c[i]+=c[i-1];
 }
 int r[maxn];
 memset(r,0,sizeof(r));
 for(int i=n-1; i>=0; --i){
 int index = c[a[i]]-1;
 r[index]=a[i];
 c[a[i]]--;
 }
 for(int i=0; i<n; ++i){
 a[i]=r[i];
 }
}

（9）基数排序

算法描述：基数排序对要排序的数据是有要求的，需要可以分割出独⽴的“位”来⽐较，⽽且位之间有递进的关系，如果 a 数据的⾼位⽐ b 数据⼤，那剩下的低位就不⽤⽐较了。除此之外，每⼀位的数据范围不能太⼤，要可以⽤线性排序算法来排序，否则，基数排序的时间复杂 度就⽆法做到 O(n) 了。

基数排序相当于通过循环进⾏了多次桶排序。

int getDigit(int x,int d){
 int t[]={1,1,10,100};
 return (x/t[d])%10;
}
void RadixSort(int *a,int begin,int end,int d){
 const int radix = 10;
 int c[maxn];
 int bucket[maxn];
 for(int k=1; k<=d; ++k){
memset(c,0,sizeof(c));
 for(int i=begin; i<=end; ++i){
 c[getDigit(a[i],k)]++;//计算i号桶⾥要放多少数
 }
 for(int i=1; i<radix; ++i) c[i]+=c[i-1];
 // 把数据依次装⼊桶（注意：装⼊时的分配技巧）
 for(int i=end; i>=begin; --i){
 int j=getDigit(a[i],k);//求出关键码的第k位的数值， 例如：576的第3
位是5
 bucket[c[j]-1]=a[i];//放⼊对应的桶中(count[j]-1)表示第k位数值为j
的桶底索引
 --c[j];//当前第k位数值为j的桶底边界索引减⼀
 }
 for(int i=begin,j=0;i<=end;++i,++j){// 从各个桶中收集数据
 a[i]=bucket[j];
 }
 }
}

（10）希尔排序

算法描述：通过将⽐较的全部元素分为⼏个区域来提升插⼊排序的性能。这样可以让⼀个元素 可以⼀次性地朝最终位置前进⼀⼤步。然后算法再取越来越⼩的步⻓进⾏排序，算法的最后⼀ 步就是普通的插⼊排序，但是到了这步，需排序的数据⼏乎是已排好的了。

// 希尔排序
void shellSort(vector<int>& nums) {
 for (int gap = nums.size() / 2; gap > 0; gap /= 2) {
 for (int i = gap; i < nums.size(); ++i) {
 for (int j = i; j - gap >= 0 && nums[j - gap] > nums[j]; j -= gap)
{
 swap(nums[j - gap], nums[j]);
 }
 }
 }
}