88、二叉树前中后遍历⼿撕代码(递归和⾮递归)
LeetCode 144. ⼆叉树的前序遍历
给你⼆叉树的根节点
示例 1:
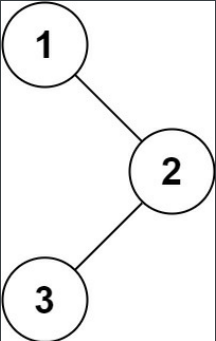
【思路】 由于“中左右”的访问顺序正好符合根结点寻找⼦节点的顺序,因此每次循环时弹栈,输出此弹 栈结点并将其右结点和左结点按照叙述顺序依次⼊栈。⾄于为什么要右结点先⼊栈,是因为栈 后进先出的特性。右结点先⼊栈,就会后输出右结点。
初始化: ⼀开始让root结点先⼊栈,满⾜循环条件
步骤: 弹栈栈顶元素,同时输出此结点 当前结点的右结点⼊栈 当前结点的左结点⼊栈重复上述过程 结束条件: 每次弹栈根结点后⼊栈⼦结点,栈为空时则说明遍历结束。
LeetCode 94. ⼆叉树的中序遍历
难度简单1035
给定⼀个⼆叉树的根节点 root ,返回它的中序遍历。
示例 1:
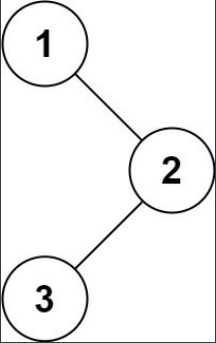
示例 2:
示例 3:
示例 4:
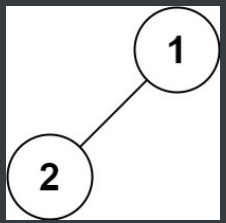
示例 5:
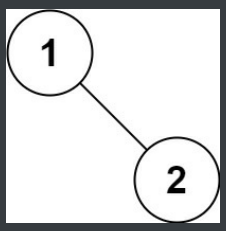
【思路】
中序遍历思路相较于前序遍历有很⼤的改变。前序遍历遇到根结点直接输出即可,但中序遍历 “左中右”需先找到此根结点的左结点,因此事实上第⼀个被输出的结点会是整个⼆叉树的最左侧结点。
依据这⼀特性,我们每遇到⼀个结点,⾸先寻找其最左侧的⼦结点,同时⽤栈记录寻找经过的 路径结点,这些是输出最左侧结点之后的返回路径。
之后每次向上层⽗结点返回,弹栈输出上层⽗结点的同时判断此结点是否含有右⼦结点,如果 存在则此右结点⼊栈并到达新的⼀轮循环,对此右结点也进⾏上述操作。 初始化: curr定义为将要⼊栈的结点,初始化为root top定义为栈顶的弹栈结点 步骤:
寻找当前结点的最左侧结点直到curr为空(此时栈顶结点即为最左侧结点)弹栈栈顶结点top并输出 判断top是否具有右结点,如果存在则令curr指向右结点,并在下⼀轮循环入栈
重复上述过程 结束条件:这⾥可以看到结束条件有两个:栈为空, curr为空。这是因为中序遍历优中后右的特性,会有⼀个时刻栈为空但右结点并未被遍历,因此只有在curr也为空证明右结点 不存在的情况下,才能结束遍历。 【代码】
LeetCode 145. ⼆叉树的后序遍历
给定⼀个⼆叉树,返回它的 后序 遍历。
示例:
进阶: 递归算法很简单,你可以通过迭代算法完成吗?
【思路】
1、前序遍历的过程是中左右。 2、将其转化成中右左。也就是压栈的过程中优先压⼊左⼦树,再压⼊右⼦树。 3、在弹栈的同时将此弹栈结点压⼊另⼀个栈,完成逆序。 4、对新栈中的元素直接顺序弹栈并输出。
【代码】
Last updated