直方图均衡化(II)

各位大家好，我是灿视，今天是是直方图均衡的第二篇～

上一篇文章，我们主要是给大家看了下直方图均衡干了什么事情，并且直接给出了，针对离散型数据的直方图均衡化的公式。

今天，我们来看下，这里面的推导过程，为什么它的公式要这么做，以及改进的两类非全局直方图均衡化～。

1. 直方图均衡公式推导

在上一篇文章，我们了解到均衡化的目的是将原始图像的直方图变为均衡分布的的形式，将一非均匀灰度概率密度分布图像，通过寻求某种灰度变换，变成一幅具有均匀概率密度分布的目的图像。我们开始以直方图均衡化的推导公式入手：

假定：$r$代表灰度级，$P(r)$为概率密度函数。$r$值已经过归一化处理，灰度值范围在$[0,1]$之间。$r$与$P(r)$之间的关系如下左图所示。均衡化的目的是将上面的非均匀分布变成如下右图所示的均匀分布：

均衡化的目的

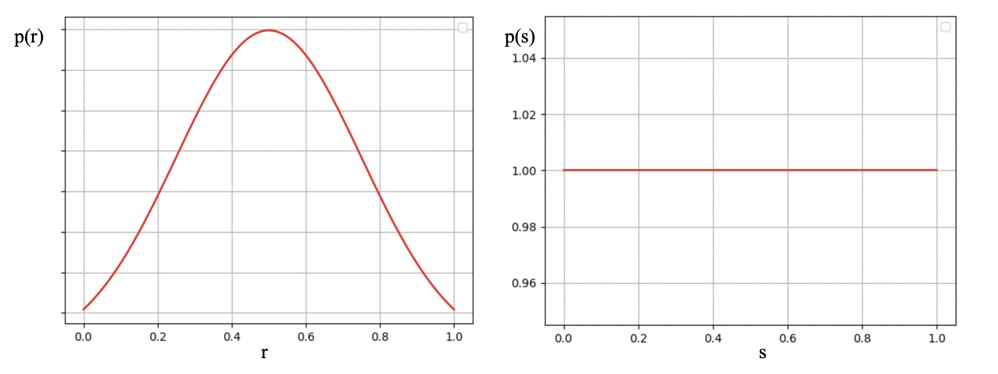
我们需要使用一种变换$S=T(r)$使直方图变平直，为使变换后的灰度仍保持从黑到白的单一变化顺序，且变换范围与原先一致，以避免整体变亮或变暗，此函数需要满足以下条件：

• 在$0 <= r <= 1$中，$T(r)$是单调递增函数，且$0 <= T(r) <= 1$；

• 反变换$\mathrm{r}=T^{-1}(\mathrm{~s}), T^{-1}(\mathrm{~s})$也为单调递增函数，且$0 <= s <= 1$。

具体的变换过程如下所示：

公式推导图示

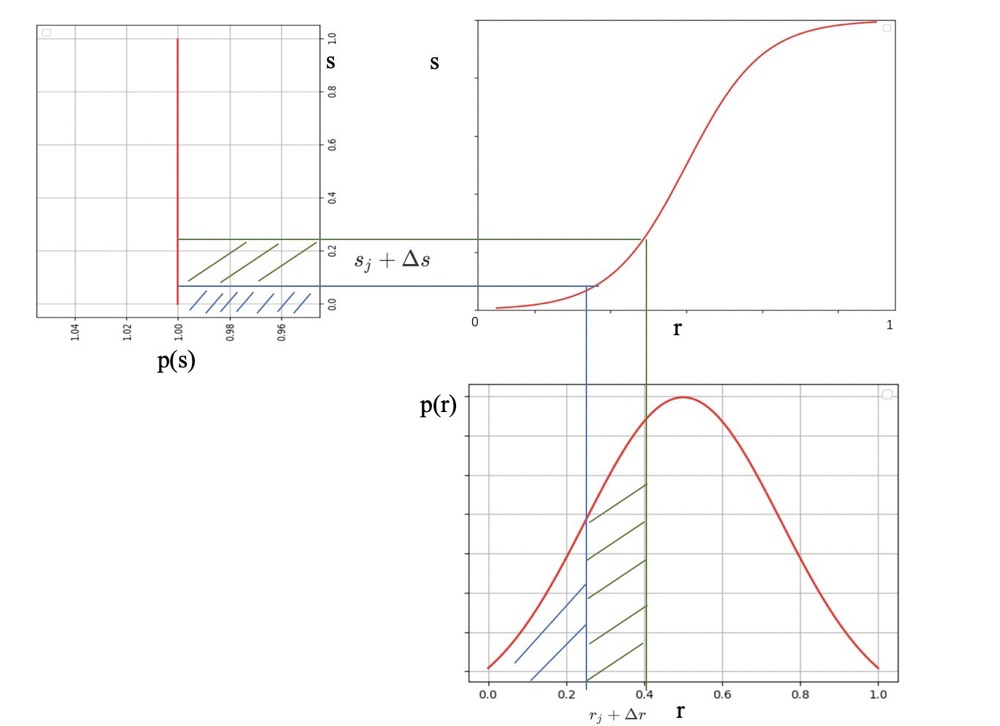
因为灰度变换不影响像素的位置分布，而且也不会增减像素数目，所以有如下的推导公式：

$$\begin{array}{l} \int_{0}^{r} p(r) d r=\int_{0}^{s} p(s) d s=\int_{0}^{s} 1 \cdot d s=s=T(r) \\ T(r)=\int_{0}^{r} p(r) d r \end{array}$$

2. 离散灰度级

因此，对于离散型的图像：

设一幅图像的像素总数为$n$，分为$L$个灰度级，其中：

$n_{k}$：表示第K个灰度级出现的个数。

$p(r_{k})=n_{k}/n$：第$K$个灰度级出现的概率。

($0<=r_{k}<=1，k=0,1,2,...,L-1$)公式如下：

$$S_{k}=T\left(r_{k}\right)=\sum_{j=0}^{k} P_{r}\left(r_{j}\right)=\sum_{j=0}^{k} \frac{n_{j}}{n}$$

因此，整个计算步骤如下：

1. 求出图像中所包含的灰度级$r_{k}$都经过归一化处理，范围在$[0,1]$之间，也可以定在$[0,L-1]$之间。

2. 统计各灰度级的像素数目$n_{k}$。

3. 计算图像直方图。

4. 计算变换函数，即$S_{k}=T\left(r_{k}\right)=\sum_{j=0}^{k} P_{r}\left(r_{j}\right)=\sum_{j=0}^{k} \frac{n_{j}}{n}$。

5. 用变换函数计算映射后输出的灰度级$s_{k}$。

6. 统计映射后新的灰度级$s_{k}$的像素数目$n_{k}$。

7. 计算输出图像的直方图。

3. 举个例子

假设有$64 * 64$大小的图像，有$8$个灰度级，灰度分布如下所示：

$$\begin{array}{ccc} r_{k} & n_{k} & P\left(r_{k}\right) \\ r_{0}=0 & 790 & 0.19 \\ r_{1}=1 / 7 & 1023 & 0.25 \\ r_{2}=2 / 7 & 850 & 0.21 \\ r_{3}=3 / 7 & 656 & 0.16 \\ r_{4}=4 / 7 & 329 & 0.08 \\ r_{5}=5 / 7 & 245 & 0.06 \\ r_{6}=6 / 7 & 122 & 0.03 \\ r_{7}=1 & 81 & 0.02 \end{array}$$

由上，我们知道该图像的$r_{k}$，$n_{k}$和$p(r_{k})$。

其中：$s_{0}=T(r_{0})=0.19$

​ $s_{1}=T(r_{1})=0.19 + 0.25=0.44$

​ $s_{2}=T(r_{2})=0.19 + 0.25 + 0.21=0.65$

​ $s_{3}=T(r_{3})=0.19 + 0.25 + 0.21 + 0.16=0.81$

​ $s_{4}=T(r_{4})=0.19 + 0.25 + 0.21 + 0.16 + 0.08=0.89$

​ $s_{5}=T(r_{2})=0.19 + 0.25 + 0.21 + 0.16 + 0.08 +0.06=0.95$

​ $s_{6}=T(r_{2})=0.19 + 0.25 + 0.21 + 0.16 + 0.08 +0.06+0.03=0.98$

​ $s_{7}=T(r_{2})=0.19 + 0.25 + 0.21 + 0.16 + 0.08 +0.06 +0.03 + 0.02=1$

由于原图像的灰度级只有8级，变换之后的$s_{k}$只能选择最接近的一个灰度级，因此需要对$s_{k}$进行舍入处理，即上述步骤中的第五步，对每个$s_{k}$将以$1/7$为量化单位进行舍入运算，结果如下：

$s_{0}=1 / 7, s_{1}=3 / 7, s_{2}=5 / 7, s_{3}=6 / 7, s_{4}=6 / 7, s_{5}=1, s_{6}=1, s_{7}=1$

根据舍入后的结果，我们可以得到均衡化后的灰度级仅有5个级别，分别是：

$s_{0}=1 / 7, s_{1}=3 / 7, s_{2}=5 / 7, s_{3}=6 / 7, s_{4}=1$

统计映射后新的灰度级 $s_{k}$ 的像素数目 $n_{k}$, 然后就可得到均衡化后的概率密度函数 $p\left(s_{k}\right)$ 。

$$\begin{array}{cccccccc} r_{k} & n_{k} & P\left(r_{k}\right) & S_{k 计算} & S_{k舍入} & S_{k} & n_{s k} & P\left(s_{k}\right) \\ r_{0}=0 & 790 & 0.19 & 0.19 & 1 / 7 & s_{0} & 790 & 0.19 \\ r_{1}=1 / 7 & 1023 & 0.25 & 0.44 & 3 / 7 & s_{1} & 1023 & 0.25 \\ r_{2}=2 / 7 & 850 & 0.21 & 0.65 & 5 / 7 & s_{2} & 850 & 0.21 \\ r_{3}=3 / 7 & 656 & 0.16 & 0.81 & 6 / 7 & & & \\ r_{4}=4 / 7 & 329 & 0.08 & 0.89 & 6 / 7 & s_{3} & 985 & 0.24 \\ r_{5}=5 / 7 & 245 & 0.06 & 0.95 & 1 & & & \\ r_{6}=6 / 7 & 122 & 0.03 & 0.98 & 1 & & & \\ r_{7}=1 & 81 & 0.02 & 1.00 & 1 & s_{4}& 448 & 0.11 \end{array}$$

因此，直方图均衡化实质上是减少图像的灰度级来加大对比度，图像经均衡化处理之后，图像变得清晰，直方图中每个像素点的灰度级减少，但分布更加均匀，对比度更高。

如上文所示的直方图均衡之后的效果：

如上图，直方图均衡化操作是对全局进行均衡化，直方图覆盖的范围太大，图片变得太亮了，反而会丢失的一些图像信息。

4. 自适应直方图均衡

在前面介绍的直方图均衡化中，是直接对全局图像进行均衡化，是$Global$ $Histogram$ $Equalization$，而没有考虑到局部图像区域($Local$ $Region$)，自适应过程就是在均衡化的过程中只利用局部区域窗口内的直方图分布来构建映射函数$f$ 。

最早的自适应直方图均衡($AHE$($Adaptive$ $Hisogram$ $Equalization$))方案如下所示：

对A图像每个像素点进行遍历，用像素点周围$W * W$的窗口进行计算直方图变换的分布函数，然后对该像素点进行映射。但首先需要对窗口大小为$W * W$的图像计算分布函数，复杂度为$O(WW + L)$ ，因此，对整张图像遍历一遍下来，复杂度为$O(MN*(W*W+L))$，复杂度太高了。

针对上面高复杂度的问题，给出了一系列改进的方案。在之前使用$W * W$的窗口来计算直方图分布函数，之后不仅对图像的一个像素点进行变换，而是将一些列(如，4， 9， 16...)像素点进行变化。若是利用$6464$的窗口来进行计算，此时采用$32 * 32$的中心区域像素点进行变换，这样的话，速度就是Naive AHE的$3232$倍。相当于在做图像分快的同时，做了直方图均衡化。

但是，这样的操作，会产生一种马赛克现象，这是因为当$W * W$窗口内像素点近似一样时，即直方图只有一个灰度级，那么这样得到的分布函数就会是一种“阶跃”的曲线，使变换后图像过度增强，一些噪声就可能被过度放大。

5. 限制对比度自适应直方图均衡化(CLAHE)

我们可以先将图像分块，每块计算一个直方图分布函数，即如下的黑丝实线边框的小块。之后，分别计算四个窗口直方图的分布函数对蓝色像素点的映射值，$f_{u l}(D), f_{u r}(D), f_{d l}(D), f_{d r}(D)$。再对其进行双线性插值，其公式如下所示：

$f(D)=(1-\Delta y)\left((1-\Delta x) f_{u l}(D)+\Delta x f_{b l}(D)\right)+\Delta y\left((1-\Delta x) f_{u r}(D)+\Delta x f_{b r}(D)\right)$ $\Delta x, \Delta y$ 是蓝色像素点相对于左上角窗口中心，即左上角黑色像素点的距离与窗口大小的比值。

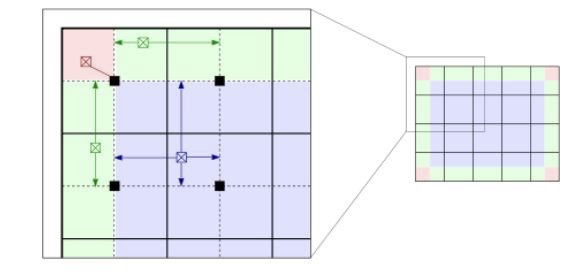
对于图中红色像素点，只使用其最近的窗口的CDF进行映射；对于图中绿色像素点，采用邻近的两个窗口的CDF映射值进行线性插值。

$CLAHE$涉及到窗口大小、影响区域大小、直方图阈值三个部分的参数，可以通过调参更好地去控制对比度增强的结果。

图像被划分后的小矩形框被称为 "tiles" (在 OpenCV 中，tileSize 默认为8x8)，在这每个小矩形框内，直方图也会被限制在一个很小的范围内（除非图像中有噪声）。

如果小区域中存在噪声，那么该噪声就会被放大，为了避免这一点，使用了对比度限制 (在 OpenCV 中，clipLimit 默认为 2.0)。

img = cv2.imread('boy.png', 0)

# create a CLAHE object
clahe = cv2.createCLAHE(clipLimit=2.0, tileGridSize=(8,8))
cl1 = clahe.apply(img)
res = np.hstack((img, cl1))
cv2.imshow("dst", res)
cv2.waitKey(0

6.自适应局部区域伸展(Local Region Stretch)直方图均衡化

上面提到的$AHE$和$CLAHE$都是基于块状区域进行直方图均衡化的，但是能不能根据灰度级 区域 近似的区域进行均衡化呢？比如对图像中灰度级$[min, max]$范围里面的所有像素点进行均衡化，使得像素点的直方图尽量在$[min, max]$上均匀分布。

因此，我们需要统计图像直方图，按照灰度级划分为三个灰度区间，使得三个区间的像素点数量近似相等，这样就分别在$[0, level1)$,$ [level1, level2)$,$ [level2, 255]$三个灰度区间做直方图均衡化，最后合并。

如下图所示：

7. 小结

这篇主要是接着上一篇文章，推导了下直方图均衡化的公式。再引出自适应直方图均衡化($AHE$) 以及 限制对比度自适应直方图均衡化($CLAHE$) 等直方图均衡化算法。

8. 参考

1. https://zhuanlan.zhihu.com/p/44918476

2. https://blog.csdn.net/qq_42593220/article/details/103227609

3. https://zhuanlan.zhihu.com/p/98541241