图像分类 $GoogLeNet$ 系列算法解读($Inception$ $V1$、$V2$、$V3$、$V4$)

看前必读

整个 $Inception$ 系列相关论文一共有四篇，在本公众号发布的$Inception$ 系列文章的文末会有四篇论文的地址，大家自行提取哈。在第一篇论文中作者提出 $Inception$ $V1$ 结构；第二篇论文提出$BN$层；第三篇论文提出$Inception$ $V2$、$V3$；第四篇论文提出$Inception$ $V4$和引入$Resnet$。本系列文主章要针对于$Inception$ $V1$、$V2$、$V3$、$V4$的结构做介绍，$BN$层以及$Inception-ResNet$将在其他文章中介绍。

$Inception$ $V1$

$Inception$ $V1$具体结构

图$1$

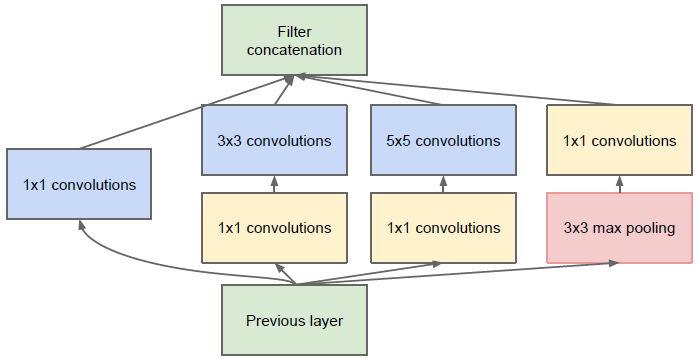
$Inception$模块的基本结构如图$1$所示，整个$GooLeNet$结构就是由多个这样的$Inception$模块串联起来的。$Inception$结构的主要贡献有两个：一是使用$1$x$1$的卷积来进行升降维；二是在多个尺寸上同时进行卷积再聚合。

从图1中可知，$Inception$块里有四条并行的路径。前三条路径使用窗口大小分别是$1$ × $1$、$3$ × $3$和 $5$ × $5$的卷积层来提取不同空间尺寸下的信息，其中中间两条路径会对输入先做$1$ × $1$卷积来减少输入通道数，以降低模型复杂度。第四条路径则使用$3$ × $3$最大池化层，后接$1$ × $1$卷积层来改变通道数。四条路径都使用了合适的填充来使输入与输出的高和宽一致。即假设输入图像为$12$ × $12$，那么四条路径输出尺寸均为$12$ × $12$，只不过输出通道数不同。每个最后我们将每条路径的输出在通道维上连结。比如，路径$1$的输出为$64$ × $12$ × $12$，路径$2$的输出为$128$ × $12$ × $12$，路径$3$的输出为$32$ × $12$ × $12$，路径$4$的输出为$32$ × $12$ × $12$，整个$Inception$块输出为($64$ + $128$ + $32$ + $32$) × $12$ × $12$。

看到这样的结构的时候，大家肯定跟我有一样的困惑，为什么这里采用并行的四条路径？为什么采用$1$×$1$的卷积核？为什么四条路径分别提取出的特征再次融合？别着急，往下看。

核心思想1：$1$×$1$卷积

作用1： 在相同尺寸的感受野中叠加更多的卷积，能提取到更丰富的特征。这个观点来自于文章$Network$ $in$ $Network$，在$Inception$ $v1$结构中的三个1x1卷积都起到了该作用。

图$2$

图$2$左图是是传统的卷积层结构（线性卷积），在一个尺度上只有一次卷积；右图是$Network$ $in$ $Network$结构（$NIN$结构），先进行一次普通的卷积（比如$3$x$3$），紧跟再进行一次$1$x$1$的卷积，对于某个像素点来说$1$x$1$卷积等效于该像素点在所有特征上进行一次全连接的计算，所以右侧图的$1$x$1$卷积画成了全连接层的形式，需要注意的是$NIN$结构中无论是第一个$3$x$3$卷积还是新增的$1$x$1$卷积，后面都紧跟着激活函数（比如$relu$）。将两个卷积串联，就能组合出更多的非线性特征。举个例子，假设第$1$个$3$x$3$卷积＋激活函数近似于$f1$($x$)=$ax2$+$bx$+$c$，第二个$1$x$1$卷积＋激活函数近似于$f2$($x$)=$mx2$+$nx$+$q$，那$f1$($x$)和$f2$($f1$($x$))比哪个非线性更强，更能模拟非线性的特征？答案是显而易见的。$NIN$的结构和传统的神经网络中多层的结构有些类似，后者的多层是跨越了不同尺寸的感受野（通过层与层中间加$pool$层），从而在更高尺度上提取出特征；$NIN$结构是在同一个尺度上的多层（中间没有$pool$层），从而在相同的感受野范围能提取更强的非线性。

作用2： 使用$1$x$1$卷积进行降维，降低了计算复杂度。在$Inception$ $v1$结构中的中间$3$x$3$卷积和$5$x$5$卷积前的$1$x$1$卷积都起到了这个作用。

图$3$

当某个卷积层输入的特征数较多，对这个输入进行卷积运算将产生巨大的计算量；如果对输入先进行降维，减少特征数后再做卷积计算量就会显著减少。图$3$是优化前后两种方案的乘法次数比较，同样是输入一组有$192$个特征、$32$x$32$大小，输出$256$组特征的数据，上面的卷积过程直接用$3$x$3$卷积实现，需要$192$x$256$x$3$x$3$x$32$x$32$=$452984832$次乘法；下面的卷积过程先用$1$x$1$的卷积降到$96$个特征，再用$3$x$3$卷积恢复出$256$组特征，需要$192$x$96$x$1$x$1$x$32$x$32$+$96$x$256$x$3$x$3$x$32$x$32$=$245366784$次乘法，使用$1$x$1$卷积降维的方法节省了将近一半的计算量。

---

核心思想2：多个尺度上进行卷积再聚合

在图1中我们可以看到对输入做了$4$个分支，分别用不同尺寸的filter进行卷积或池化，最后再在特征维度上拼接到一起。这种全新的结构有什么好处呢？

解释1： 在直观感觉上在多个尺度上同时进行卷积，能提取到不同尺度的特征。特征更为丰富也就意味着最后分类判断时更加准确。

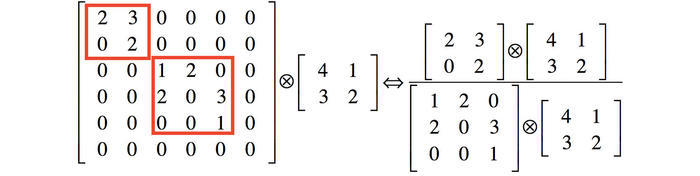
解释2： 利用稀疏矩阵分解成密集矩阵计算的原理来加快收敛速度。举个例子，图$4$左侧是个稀疏矩阵（很多元素都为$0$，不均匀分布在矩阵中），和一个$2$x$2$的矩阵进行卷积，需要对稀疏矩阵中的每一个元素进行计算；如果像右图那样把稀疏矩阵分解成$2$个子密集矩阵，再和$2$x$2$矩阵进行卷积，稀疏矩阵中$0$较多的区域就可以不用计算，计算量就大大降低。这个原理应用到inception上就是要在特征维度上进行分解！传统的卷积层的输入数据只和一种尺度（比如$3$x$3$）的卷积核进行卷积，输出固定维度（比如$256$个特征）的数据，所有$256$个输出特征基本上是均匀分布在$3$x$3$尺度范围上，这可以理解成输出了一个稀疏分布的特征集；而$inception$模块在多个尺度上提取特征（比如$1$x$1$，$3$x$3$，$5$x$5$），输出的$256$个特征就不再是均匀分布，而是相关性强的特征聚集在一起（比如$1$x$1$的的$96$个特征聚集在一起，$3$x$3$的$96$个特征聚集在一起，$5$x$5$的$64$个特征聚集在一起），这可以理解成多个密集分布的子特征集。这样的特征集中因为相关性较强的特征聚集在了一起，不相关的非关键特征就被弱化，同样是输出$256$个特征，$inception$方法输出的特征“冗余”的信息较少。用这样的“纯”的特征集层层传递最后作为反向计算的输入，自然收敛的速度更快。

图$4$

---

核心思想3：辅助$softmax$

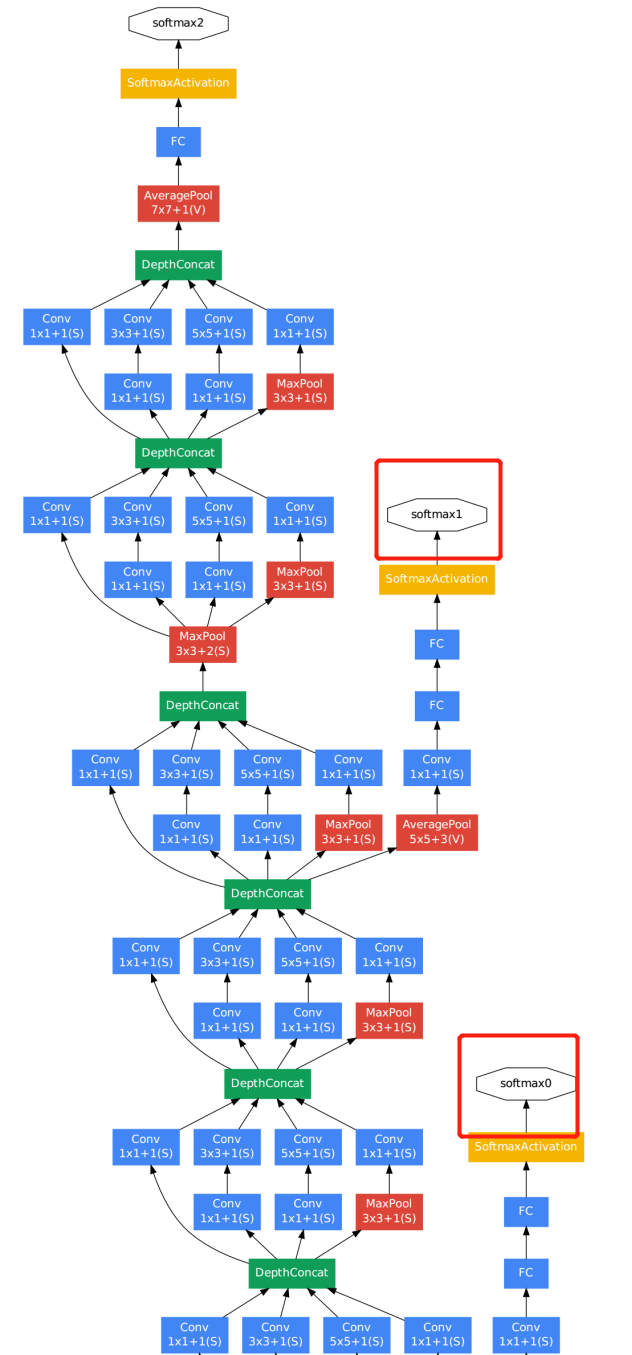
网络的中间部位还输出了另外两个辅助的$softmax$，如图$5$中的$softmax0$和$softmax1$，其作用是增强低层网络的判别能力，增强反向传播的梯度的大小，提供额外的正则化能力；在训练过程中，损失值是最后层的$softmax loss$加0.3×中间输出的$softmax$ $loss$，推理时，忽略中间的两个$softmax$输出。

图$5$

在这里给出I$nception$ $V1$的代码

import torch.nn as nn
import torch
import torch.nn.functional as F

# Inception代表上述的模块；InceptionAux代表的是分支预测；
class GoogLeNet(nn.Module):
    def __init__(self, num_classes=1000, aux_logits=True, init_weights=False):
        super(GoogLeNet, self).__init__()
        self.aux_logits = aux_logits

        self.conv1 = BasicConv2d(3, 64, kernel_size=7, stride=2, padding=3)
        self.maxpool1 = nn.MaxPool2d(3, stride=2, ceil_mode=True)

        self.conv2 = BasicConv2d(64, 64, kernel_size=1)
        self.conv3 = BasicConv2d(64, 192, kernel_size=3, padding=1)
        self.maxpool2 = nn.MaxPool2d(3, stride=2, ceil_mode=True)

        self.inception3a = Inception(192, 64, 96, 128, 16, 32, 32)
        self.inception3b = Inception(256, 128, 128, 192, 32, 96, 64)
        self.maxpool3 = nn.MaxPool2d(3, stride=2, ceil_mode=True)

        self.inception4a = Inception(480, 192, 96, 208, 16, 48, 64)
        self.inception4b = Inception(512, 160, 112, 224, 24, 64, 64)
        self.inception4c = Inception(512, 128, 128, 256, 24, 64, 64)
        self.inception4d = Inception(512, 112, 144, 288, 32, 64, 64)
        self.inception4e = Inception(528, 256, 160, 320, 32, 128, 128)
        self.maxpool4 = nn.MaxPool2d(3, stride=2, ceil_mode=True)

        self.inception5a = Inception(832, 256, 160, 320, 32, 128, 128)
        self.inception5b = Inception(832, 384, 192, 384, 48, 128, 128)

        if self.aux_logits:
            self.aux1 = InceptionAux(512, num_classes)
            self.aux2 = InceptionAux(528, num_classes)

        self.avgpool = nn.AdaptiveAvgPool2d((1, 1))
        self.dropout = nn.Dropout(0.4)
        self.fc = nn.Linear(1024, num_classes)
        if init_weights:
            self._initialize_weights()

    def forward(self, x):
        # N x 3 x 224 x 224
        x = self.conv1(x)
        # N x 64 x 112 x 112
        x = self.maxpool1(x)
        # N x 64 x 56 x 56
        x = self.conv2(x)
        # N x 64 x 56 x 56
        x = self.conv3(x)
        # N x 192 x 56 x 56
        x = self.maxpool2(x)

        # N x 192 x 28 x 28
        x = self.inception3a(x)
        # N x 256 x 28 x 28
        x = self.inception3b(x)
        # N x 480 x 28 x 28
        x = self.maxpool3(x)
        # N x 480 x 14 x 14
        x = self.inception4a(x)
        # N x 512 x 14 x 14
        if self.training and self.aux_logits:    # eval model lose this layer
            aux1 = self.aux1(x)

        x = self.inception4b(x)
        # N x 512 x 14 x 14
        x = self.inception4c(x)
        # N x 512 x 14 x 14
        x = self.inception4d(x)
        # N x 528 x 14 x 14
        if self.training and self.aux_logits:    # eval model lose this layer
            aux2 = self.aux2(x)

        x = self.inception4e(x)
        # N x 832 x 14 x 14
        x = self.maxpool4(x)
        # N x 832 x 7 x 7
        x = self.inception5a(x)
        # N x 832 x 7 x 7
        x = self.inception5b(x)
        # N x 1024 x 7 x 7

        x = self.avgpool(x)
        # N x 1024 x 1 x 1
        x = torch.flatten(x, 1)
        # N x 1024
        x = self.dropout(x)
        x = self.fc(x)
        # N x 1000 (num_classes)
        if self.training and self.aux_logits:   # eval model lose this layer
            return x, aux2, aux1
        return x

    def _initialize_weights(self):
        for m in self.modules():
            if isinstance(m, nn.Conv2d):
                nn.init.kaiming_normal_(m.weight, mode='fan_out', nonlinearity='relu')
                if m.bias is not None:
                    nn.init.constant_(m.bias, 0)
            elif isinstance(m, nn.Linear):
                nn.init.normal_(m.weight, 0, 0.01)
                nn.init.constant_(m.bias, 0)


class Inception(nn.Module):
    def __init__(self, in_channels, ch1x1, ch3x3red, ch3x3, ch5x5red, ch5x5, pool_proj):
        super(Inception, self).__init__()

        self.branch1 = BasicConv2d(in_channels, ch1x1, kernel_size=1)

        self.branch2 = nn.Sequential(
            BasicConv2d(in_channels, ch3x3red, kernel_size=1),
            BasicConv2d(ch3x3red, ch3x3, kernel_size=3, padding=1)   # 保证输出大小等于输入大小
        )

        self.branch3 = nn.Sequential(
            BasicConv2d(in_channels, ch5x5red, kernel_size=1),
            BasicConv2d(ch5x5red, ch5x5, kernel_size=5, padding=2)   # 保证输出大小等于输入大小
        )

        self.branch4 = nn.Sequential(
            nn.MaxPool2d(kernel_size=3, stride=1, padding=1),
            BasicConv2d(in_channels, pool_proj, kernel_size=1)
        )

    def forward(self, x):
        branch1 = self.branch1(x)
        branch2 = self.branch2(x)
        branch3 = self.branch3(x)
        branch4 = self.branch4(x)

        outputs = [branch1, branch2, branch3, branch4]
        # 由于pytorch的数据格式是(n,c,h,w)，矩阵聚合的时候需要在c的维度上进行
        # 因此这里的torch.cat中的dim=1。
        return torch.cat(outputs, 1)


class InceptionAux(nn.Module):
    def __init__(self, in_channels, num_classes):
        super(InceptionAux, self).__init__()
        self.averagePool = nn.AvgPool2d(kernel_size=5, stride=3)
        # 这里的BasicConv2d是conv2D+BN
        self.conv = BasicConv2d(in_channels, 128, kernel_size=1)  # output[batch, 128, 4, 4]

        self.fc1 = nn.Linear(2048, 1024)
        self.fc2 = nn.Linear(1024, num_classes)

    def forward(self, x):
        # aux1: N x 512 x 14 x 14, aux2: N x 528 x 14 x 14
        x = self.averagePool(x)
        # aux1: N x 512 x 4 x 4, aux2: N x 528 x 4 x 4
        x = self.conv(x)
        # N x 128 x 4 x 4
        x = torch.flatten(x, 1)
        x = F.dropout(x, 0.5, training=self.training)
        # N x 2048
        x = F.relu(self.fc1(x), inplace=True)
        x = F.dropout(x, 0.5, training=self.training)
        # N x 1024
        x = self.fc2(x)
        # N x num_classes
        return x


class BasicConv2d(nn.Module):
    def __init__(self, in_channels, out_channels, **kwargs):
        super(BasicConv2d, self).__init__()
        self.conv = nn.Conv2d(in_channels, out_channels, **kwargs)
        self.relu = nn.ReLU(inplace=True)

    def forward(self, x):
        x = self.conv(x)
        x = self.relu(x)
        return x

总结

一方面$Inception$ $V1$采用了$Inception$这样的模块去提取不同尺度下的特征信息，并使用了$1$×$1$的卷积核满足了在相同尺寸的感受野中提取到更丰富的特征的同时降低了计算量。

另一方面以多个尺度上进行卷积再聚合的方式在多个尺度上同时进行卷积，提取不同尺度的特征进行融合进而提升最后的分类准确度，并且加快模型训练时的收敛速度。

最后也使用了辅助损失函数，增强低层网络的判别能力的同时，增强反向传播的梯度的大小，提供额外的正则化能力。

• https://arxiv.org/abs/1409.4842

• https://arxiv.org/pdf/1312.4400.pdf

• https://zhuanlan.zhihu.com/p/30172532

• https://www.cnblogs.com/shouhuxianjian/p/7786760.html

• https://blog.csdn.net/qq_35605081/article/details/110843720

• https://www.linkedin.com/pulse/receptive-field-effective-rf-how-its-hurting-your-rosenberg

• https://blog.csdn.net/qq_32172681/article/details/99977304?utm_medium=distribute.pc_relevant.none-task-blog-baidujs_title-1&spm=1001.2101.3001.4242