add_with_concat

阅读原文

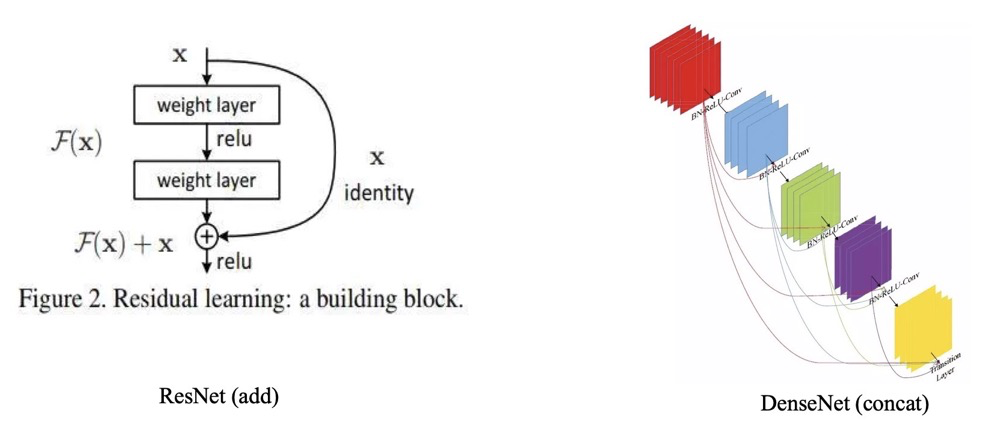
特征融合目前有两种常用的方式，一种是$add$操作，这种操作广泛运用于$ResNet$与$FPN$中。一种是$Concat$操作，这种操作最广泛的运用就是$UNet$，$DenseNet$等网络中。如下图所示：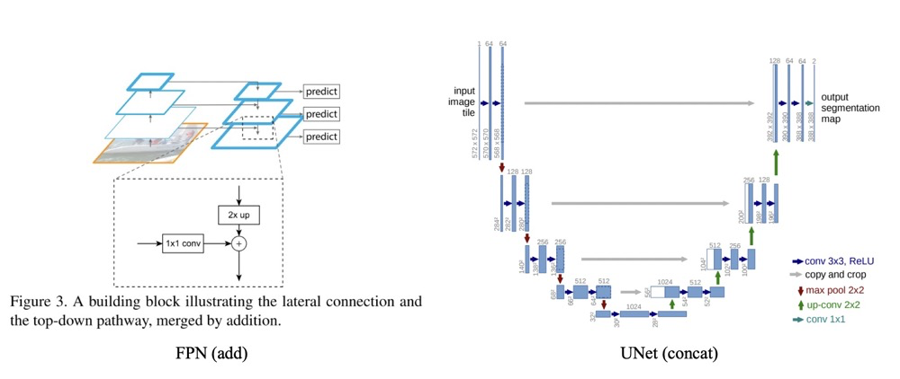

也有如$HRNet$这样的，多分辨率之间使用$add$形式的特征融合。

代码演示

>>> import torch
>>> img1 = torch.randn(2, 3, 58, 58)
>>> img2 = torch.randn(2, 3, 58, 58)
>>> img3 = img1 + img2
>>> img4 = torch.cat((img1, img2), dim=1)
>>> img3.size()
torch.Size([2, 3, 58, 58])
>>> img4.size()
torch.Size([2, 6, 58, 58])
>>>

那么对于$Add$操作与$Concat$操作，它们中间有哪些区别与联系呢？

联系

$add$ 和$concat$ 形式都可以理解为整合多路分支$feature$ $map$ 的信息，只不过$concat$ 比较直观(同时利用不同层的信息)，而$add$ 理解起来比较生涩(为什么两个分支的信息可以相加？)。$concat$ 操作时时将通道数增加，$add$ 是特征图相加，通道数不变。

对于两路通入而言，其大小($H, W$ )是一样的。假设两路输入的通道分别为$X_{1}, X_{2}, … X_{c}$， $Y_{1}, Y_{2},…Y_{n}$。

则对于$Concat$的操作，通道数相同且后面带卷积的话，$add$等价于$concat$之后对应通道共享同一个卷积核。

当我们需要聚合的两个分支的$Feature$叫做$X$与$Y$的时候，我们可以使用$Concat$, 概括为：

$$Z_{out}=\sum_{i=1}^{c} X_{i} * K_{i}+\sum_{i=1}^{c} Y_{i} * K_{i+c}$$

对于$add$的操纵，可以概括为：

$$Z_{\text {add }}=\sum_{i=1}^{c}\left(X_{i}+Y_{i}\right) * K_{i}=\sum_{i=1}^{c} X_{i} * K_{i}+\sum_{i=1}^{c} Y_{i} * K_{i}$$

因此，采用$add$操作，我们相当于加入一种先验。当两个分支的特征信息比较相似，可以用$add$来代替$concat$，这样可以更节省参数量。

区别

• 对于$Concat$操作而言，通道数的合并，也就是说描述图像本身的特征增加了，而每一特征下的信息是没有增加。

• 对于$add$层更像是信息之间的叠加。这里有个先验，$add$前后的$tensor$语义是相似的。

结论

因此，像是需要将$A$与$B$的$Tensor$进行融合，如果它们语义不同，则我们可以使用$Concat$的形式，如$UNet$, $SegNet$这种编码与解码的结构，主要还是使用$Concat$。

而如果$A$与$B$是相同语义，如$A$与$B$是不同分辨率的特征，其语义是相同的，我们可以使用$add$来进行融合，如$FPN$等网络的设计。