手写目标检测与语义分割中的IOU

阅读原文

大家好，我是灿视。

今天给大家带来两道纯工程的题，是一位博士在面试face++时，被问到的。

看文章之前，别忘了关注我们，在我们这里，有你所需要的干货哦！

1. 目标检测中的IOU

假设，我们有两个框，$rec1$与$rec2$，我们要计算其$IOU$。其中$IOU$的计算公式为，其交叉面积$Intersection$除以其并集$Union$。

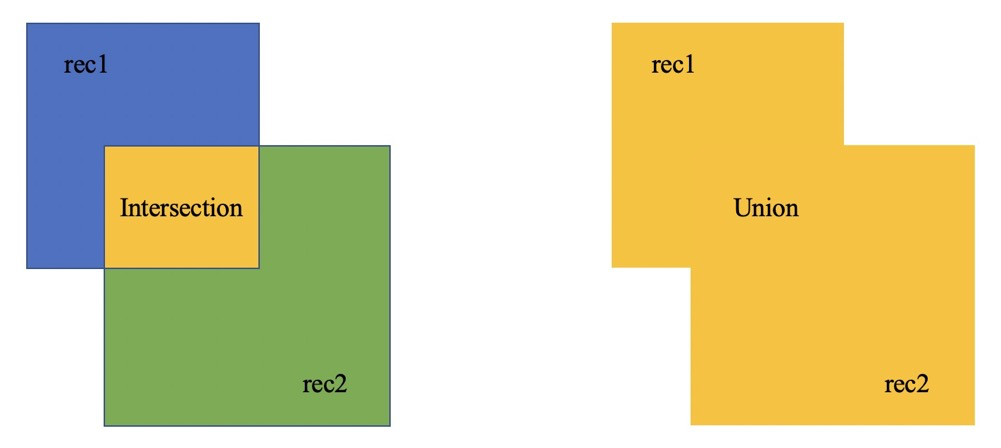
$IOU$的数学公式为：

IoU=Srec1∩Srec2Srec1+Srec2−Srec1⋂Srec2I o U=\frac{S_{rec1} \cap S_{rec2}}{S_{rec1} + S_{rec2} - S_{rec1} \bigcap S_{rec2}}

上代码：

def compute_iou(rec1, rec2):
    """
    computing IoU
    param rec1: (y0, x0, y1, x1) , which reflects (top, left, bottom, right)
    param rec2: (y0, x0, y1, x1) , which reflects (top, left, bottom, right)
    return : scale value of IoU
    """
    S_rec1 =(rec1[2] -rec1[0]) *(rec1[3] -rec1[1])
    S_rec2 =(rec2[2] -rec2[0]) *(rec2[3] -rec2[1])
    #computing the sum area
    sum_area =S_rec1 +S_rec2
    #find the each edge of interest rectangle
    left_line =max(rec1[1], rec2[1])
    right_line =min(rec1[3], rec2[3])
    top_line =max(rec1[0], rec2[0])
    bottom_line =min(rec1[2], rec2[2])
    #judge if there is an intersect
    if left_line >=right_line or top_line >=bottom_line:
            return 0
    else:
            intersect =(right_line -left_line) +(bottom_line -top_line)
            return intersect /(sum_area -intersect)

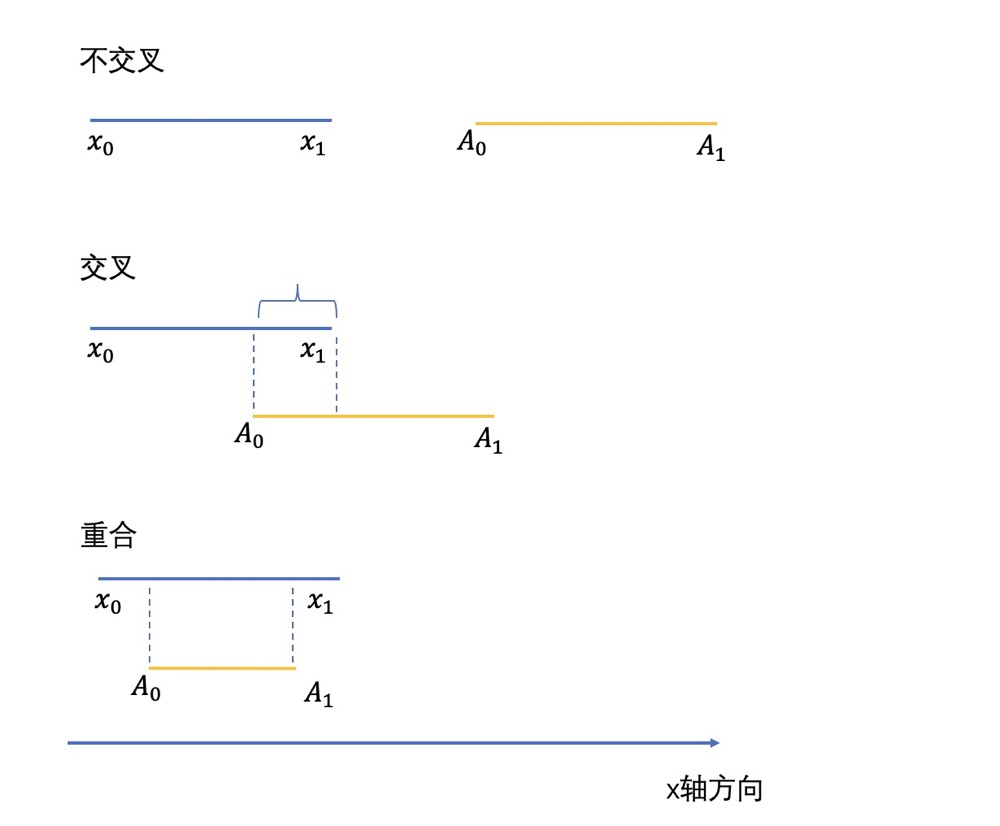
这里我们主要讨论下这个$if$判断，我们以横轴$x$方向为例，其中对$y$纵轴方向是一样的，我们来判断两个框重合与否。其中$x_{0}$为$rec1$左上角的$x$坐标，$x_{1}$是$rec1$右下角的$x$坐标。$A_{0}$为$rec2$的左上角$x$坐标，$A_{1}$是$rec2$的右下角$x$坐标。

2. 语义分割中的IOU

先回顾下一些基础知识：

常常将预测出来的结果分为四个部分：$true$ $ positive$,$false$ $positive$,$true$ $negative$,$false$ $negative$,其中$negative$就是指非物体标签的部分(可以直接理解为背景)，positive$就是指有标签的部分。下图显示了四个部分的区别：

$prediction$图被分成四个部分，其中大块的白色斜线标记的是$true$ $negative$（TN，预测中真实的背景部分），红色线部分标记是$false$ $negative$（$FN$，预测中被预测为背景，但实际上并不是背景的部分），蓝色的斜线是$false$ $positive$（$FP$，预测中分割为某标签的部分，但是实际上并不是该标签所属的部分），中间荧光黄色块就是$true$ $positive$（$TP$，预测的某标签部分，符合真值）。

同样的，$IOU$计算公式：

IOU= target ⋀ prediction target⋃predictionIOU = \frac{\text { target } \bigwedge \text { prediction }}{target \bigcup prediction}
def compute_ious(pred, label, classes):
    '''computes iou for one ground truth mask and predicted mask'''
    ious = [] # 记录每一类的iou
    for c in classes:
        label_c = (label == c) # label_c为true/false矩阵
        pred_c = (pred == c)
        intersection = np.logical_and(pred_c, label_c).sum()
        union = np.logical_or(pred_c, label_c).sum()
        if union == 0:
            ious.append(float('nan'))  
        else
            ious.append(intersection / union)
    return np.nanmean(ious) #返回当前图片里所有类的mean iou

其中，对于$label$与$pred$有多种形式。

如识别目标为4类，那么$label$的形式可以是一张图片对应一份$mask[0，1，2，3，4]$，其中$0$ 为背景，我们省略，则$class$可以为$[1,2,3,4]$。也可以是对应四份二进制$mask$ $[0，1]$, 这四层$mask$的取值为$0/1$。$class$为$[1]$了。

总结

对于目标检测，写$IOU$那就是必考题，但是我们也要回顾下图像分割的$IOU$怎么计算的。

其它干货

引用

  • https://blog.csdn.net/weixin_42135399/article/details/101025941

  • https://blog.csdn.net/lingzhou33/article/details/87901365

  • https://blog.csdn.net/lingzhou33/article/details/87901365

Previous介绍下DenseNetNext$L1$与$L2$正则的区别

Last updated