sigmoid与softmax的区别与联系

阅文原文

Softmax与Sigmoid有哪些区别与联系？

1. Sigmoid函数

$Sigmoid$函数也叫$Logistic$函数，将输入值压缩到$(0,1)$区间之中，其函数表达式为：

Sigmoid(x)=11+e−xSigmoid(x) =\frac{1}{1+e^{-x}}

函数图像如图所示：

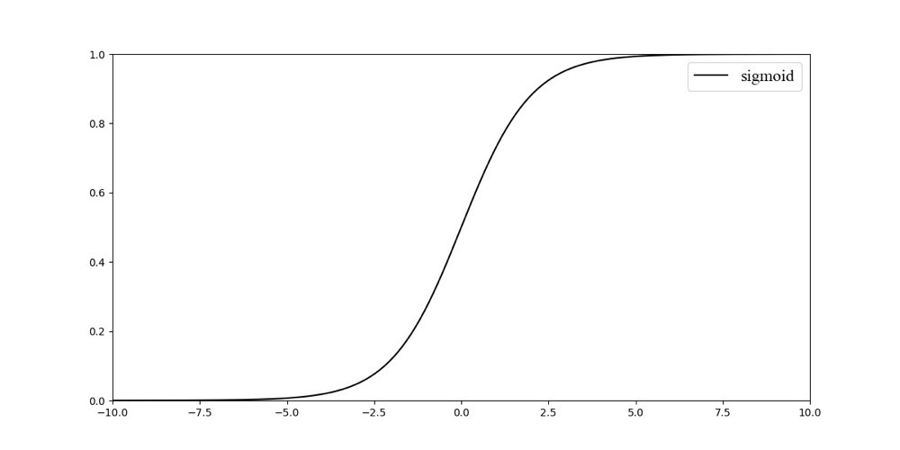
image-20210503121004018

其求导之后的表达式为：

Sigmoid⁡′(x)=Sigmoid⁡(x)⋅(1−Sigmoid⁡(x))\operatorname{Sigmoid}^{\prime}(x)=\operatorname{Sigmoid}(x) \cdot(1-\operatorname{Sigmoid}(x))

其梯度的导数图像如：

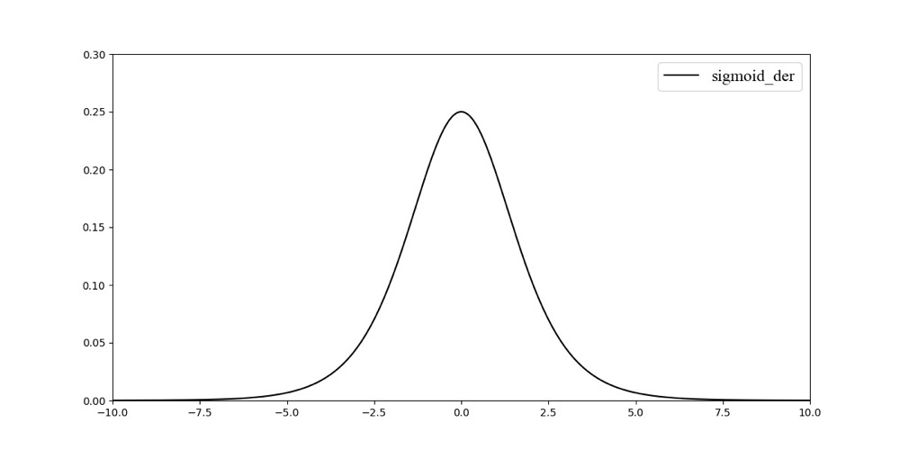
image-20210503121145452

对于$Sigmoid$函数，其优点为：

  • $Sigmoid$函数的输出在$(0,1)$之间，我们通常把它拿来作为一个二分类的方案。其输出范围有限，可以用作输出层,优化稳定。

  • $Sigmoid$函数是一个连续函数，方便后续求导。

其缺点为：

  • 从函数的导函数可以得到，其值范围为(0, 0.25)，存在梯度消失的问题。

  • $Sigmoid$函数不是一个零均值的函数，导致后一层的神经元将得到上一层非$0$均值的信号作为输入，从而会对梯度产生影响。

  • $Sigmoid$函数是一个指数函数的激活函数，我们把每次基本运算当作一次$FLOPs$(Floating Point Operations Per Second)，则$Sigmod$函数包括求负号，指数运算，加法与除法等4$FLOPs$的运算量，预算量较大。而如$Relu(x)=max(0, x)$，为$1FLOPs$。

**对于非互斥的多标签分类任务，且我们需要输出多个类别。如一张图我们需要输出是否是男人，是否戴了眼镜，我们可以采用$Sigmoid$函数来输出最后的结果。**如最后$Sigmoid$的输出为$[0.01, 0.02, 0.41, 0.62, 0.3, 0.18, 0.5, 0.42, 0.06, 0.81]$，我们通过设置一个概率阈值，比如$0.3$，如果概率值大于$0.3$，则判定类别符合，那么该输入样本则会被判定为类别$3$、类别$4$、类别$5$、类别$7$及类别$8$，即一个样本具有多个标签。

2. Softmax函数

$Softmax$函数又称归一化指数函数，函数表达式为：

yi=Softmax⁡(xi)=exi∑j=1nexjy_{i}=\operatorname{Softmax}(x_{i})=\frac{e^{x_{i}}}{\sum_{j=1}^{n} e^{x_{j}}}

其中，$i \in [1, n]$。$\sum_{i} y_{i}=1$。如网络输出为$[-20, 10, 30]$，则经过$Softmax$层之后，输出为$[1.9287e-22, 2.0612e-09, 1.0000e+00]$。

对于$Softmax$，往往我们会在面试的时候，需要手写$Softmax$函数，这里给出一个参考版本。

import numpy as np
def softmax( f ):
    # 为了防止数值溢出，我们将数值进行下处理
    # f： 输入值
    f -= np.max(f) # f becomes [-666, -333, 0]
    return np.exp(f) / np.sum(np.exp(f))

针对$Softmax$函数的反向传播，这里给出手撕反传的推导过程，主要是分两种情况：

image

因此，不失一般性，扩展成矩阵形式则为：

$\frac{\partial Y}{\partial X}=\operatorname{diag}(Y)-Y^{T} \cdot Y($ 当Y的shape为 $(1, \mathrm{n})$ 时)。后面在下一题中，我们会将$Softmax$与$Cross$ $Entropy$ $Loss$进行结合，再来推导前向与反向。

因此，当我们的任务是一个互斥的多类别分类任务（如imagenet分类），网络只能输出一个正确答案，我们可以用$Softmax$函数处理各个原始的输出值。从公式中，我们可以看到$Softmax$函数的分母是综合到了所有类别的信息。通常我们也会把$Softmax$函数的输出，这主要是由于$Softmax$函数先拉大了输入向量元素之间的差异（通过指数函数），然后才归一化为一个概率分布，在应用到分类问题时，它使得各个类别的概率差异比较显著，最大值产生的概率更接近$1$，这样输出分布的形式更接近真实分布当作网络的置信度。

对于$Softmax$函数而言，我们可以从不同的角度来理解它：

  • $Argmax$是一个暴力的找最大值的过程，最后的输出是以一个$One-hot$形式，将最大值的位置设置为$1$，其余为$0$。这样的话，则在网络训练中，是不可导的，我们采用$Softmax$看作是$Argmax$的平滑近似，从而可以使得网络可导。

  • $Softmax$将输入向量归一化映射到一个类别概率分布，即$n$个类别上的概率分布，因此我们常将$Softmax$放到$MLP$ 的最后一层。

  • 从概率图角度，$Softmax$可以理解为一个概率无向图上的联合概率。

3. 联系

对于二分类任务而言，二者都可以达到目标，在理论上，没有什么区别。

举个栗子，如现在是二分类($x_{1},x_{2}$), 经过$Sigmoid$函数之后：

Sigmoid⁡(x1)=11+e−x1\operatorname{Sigmoid}\left(x_{1}\right)=\frac{1}{1+e^{-x_{1}}}

对于$Softmax$函数，则为：

Softmax⁡(x1)=ex1ex1+ex2=11+e−(x1−x2)\operatorname{Softmax}\left(x_{1}\right)=\frac{e^{x_{1}}}{e^{x_{1}}+e^{x_{2}}}=\frac{1}{1+e^{-\left(x_{1}-x_{2}\right)}}

对于$x_{1} - x_{2}$,我们可以使用一个$z_{1}$来进行替换，则替换成了：

Softmax⁡(x1)=11+e−z1\operatorname{Softmax}\left(x_{1}\right)=\frac{1}{1+e^{-z_{1}}}

该表达式与$Sigmoid(x_{1})$相同，理论上是相同的。

4. 区别

在我们进行二分类任务时，当我们使用$Sigmoid$函数，最后一层全连接层的神经元个数是$1$，神经网络的输出经过它的转换，可以将数值压缩到$(0,1)$之间，得到的结果可以理解成分类成目标类别的概率$P$，而不分类到该类别的概率是$(1 - P)$，这也是典型的两点分布的形式。

而使用$Softmax$函数则需要是两个神经元，一个是表示前景类的分类概率，另一个是背景类。此时，$Softmax$函数也就退化成了二项分布。

更简单一点理解，$Softmax$函数是对两个类别进行建模，其两个类别的概率之和是$1$。而$Sigmoid$ 函数是对于一个类别的建模，另一个类别可以通过1来相减得到。

$Sigmoid$得到的结果是“分到正确类别的概率和未分到正确类别的概率”，$Softmax$得到的是“分到正确类别的概率和分到错误类别的概率”。

PreviousresnetNextsoftmax及其相关变形

Last updated