$L1$与$L2$正则的区别

正则化($Regularization$) 是机器学习中对原始损失函数引入惩罚项，以防止过拟合或提高模型泛化性能的一类方法的统称。所谓惩罚是指对损失函数中的某些参数做一些限制。此时目标函数变成了原始损失函数+惩罚项，常用的正则项一般有两种，英文称作$l_{1}−norm$和$l_{2}−norm$，中文称作$L1$正则化和$L2$正则化，或者$L1$范数和$L2$范数（实际是$L2$范数的平方）。

对于线性回归模型，使用$L1$正则化的模型叫做$Lasso$回归，使用$L2$正则化的模型叫做$Ridge$回归（岭回归）。

1. $L1$正则化

假设带有$L1$正则化的目标函数为： J=J0+∣∣W∣∣1=J0+α∑∣w∣         (1)J=J_0 + ||W||_1 = J_0 + \alpha\sum|w|\ \ \ \ \ \ \ \ \ (1)

其中，$J_0$为原始的损失函数，$\alpha \sum |w|$为L1正则化项，$\alpha$为正则化系数，$w$ 表示特征的系数（x的参数），可以看到正则化项是对系数做了限制。L1正则化是指权值向量$w$中各个元素的绝对值之和，通常表示为$||w||_1$

$L1$范数符合拉普拉斯分布，是不完全可微的。表现在图像上会有很多角出现。这些角和目标函数的接触机会远大于其他部分。就会造成最优值出现在坐标轴上，因此就会导致某一维的权重为$0$ ，产生稀疏权重矩阵，进而防止过拟合。

$L1$正则化项相当于对原始损失函数$J_0$做了一个约束。我们令$L = \alpha\sum|w|$，那么整个目标函数可以写成：

J=J0+L     (2)J= J_0 + L \ \ \ \ \ (2)

我们的目的就是求出在约束条件$L$下，$J_0$取最小值的解。为了方便理解，我们考虑二维的情况，此时$L = |w_1| + |w_2|$

L1正则化图示

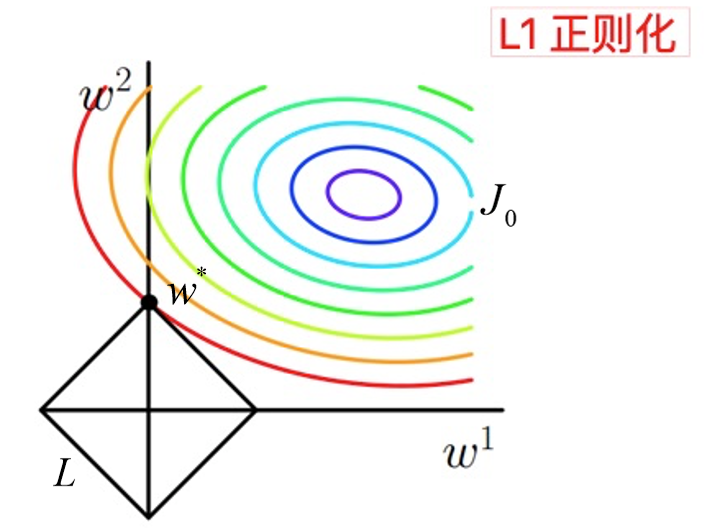
图中等高线是 $J_0$ 的等高线，黑色菱形是 $L$ 函数的图形。图中当等高线 $J_0$ 与 $L$ 图形首次相交的地方就是最优解。上图中 $J_0$ 与 $L$ 在一个顶点处相交，这个顶点就是最优解 $w^∗$。

拓展到多维，$L$ 函数就会有很多突出的角（二维情况下四个，多维情况下更多），$J_0$ 与这些角接触的概率远大于与 $L$ 其它部位接触的概率（这是很直觉的想象，突出的角比直线的边离等值线更近），而在这些角的位置上使很多权重为0。所以在最优解处，L1正则化就可以产生稀疏模型，进而可以用于特征选择。

$\alpha$正则化系数，可以控制 $L$ 图形的大小，$\alpha$越小，$L$ 图形越大，$\alpha$越大，$L$ 图形越小。

$L1$正则化对所有参数的惩罚力度都一样，可以让一部分权重变为$0$，去除某些特征（权重为0则等效于去除），因此产生稀疏模型。

那么稀疏模型有什么好处呢？

稀疏化正则化项一个最重要的优势就在于实现特征的自动选择。所谓稀疏性，说白了就是模型的很多参数是0。通常机器学习中特征数量很多，例如文本处理时，如果将一个词组（$term$）作为一个特征，那么特征数量会达到上万个（$bigram$）。但是只有少数特征对该模型有贡献，绝大部分特征是没有贡献的。在最小化目标函数时，需要考虑这些额外的特征，虽然能获得更小的训练误差，但在预测阶段，模型会考虑这些无用的特征，从而可能干扰模型的正确预测。

这种模型就是所谓的泛化性能不强，有过拟合的嫌疑。如果通过稀疏化正则化项得到一个稀疏模型，很多参数是$0$，此时我们就可以只关注系数是非零值的特征。这相当于对模型进行了一次特征选择，只留下一些比较重要的特征，提高模型的泛化能力，降低过拟合的可能。这就是稀疏模型与特征选择的关系。

2. $L2$正则化

假设带有$L2$正则化的目标函数为：

J=J0+∣∣w∣∣22=J0+α∑w2         (3)J = J_0 + ||w||^2_2 = J_0+\alpha \sum w^2 \ \ \ \ \ \ \ \ \ (3)

同$L1$正则化，$w$ 表示特征的系数（$x$的参数），可以看到正则化项是对系数做了限制。$L2$正则化是指权值向量$w$中各个元素的平方和然后再求平方根（可以看到$Ridge$回归的$L2$正则化项有平方符号），通常表示为$||w||_2$

$L2$范数符合高斯分布，是完全可微的。和$L1$相比，图像上为一个⚪。一般最优值不会在坐标轴上出现。在最小化正则项时，参数不断趋向于$0$，但并不是$0$。

如下图：

L2正则化图示 相比于$L1$正则化，$L2$正则化的函数 $L$ 与 $J_0$ 第一次相交的地方出现在具有稀疏性的位置的概率就变得非常小了。这就从直观上来解释了为什么$L1$正则化能产生稀疏性，而$L2$正则化不能产生稀疏性的原因了。

$L2$正则化的作用：主要是为了防止过拟合。

拟合过程中通常都倾向于让权值尽可能小，最后构造一个所有参数都比较小的模型。因为一般认为参数值小的模型比较简单，泛化能力强，能适应不同的数据集，也在一定程度上避免了过拟合现象。可以设想一下对于一个线性回归方程，若参数很大，那么只要数据偏移一点点，就会对结果造成很大的影响；但如果参数足够小，数据偏移得多一点也不会对结果造成什么影响，专业一点的说法是抗扰动能力强。

越是复杂的模型，越是尝试对所有样本进行拟合，包括异常点。这就会造成在较小的区间中产生较大的波动，这个较大的波动也会反映在这个区间的导数比较大。只有越大的参数才可能产生较大的导数。因此参数越小，模型就越简单。

为什么$L2$正则化能够得到值很小的参数？？？

我们通过线性回归，来看一下$L2$正则化解决过拟合问题。

假设要求解的参数为$\theta$，$h_{\theta}(x)$ 是假设函数。线性回归一般使用平方差损失函数。单个样本的平方差是$h_{\theta}(x) - y)^2$，如果考虑所有样本，损失函数是对每个样本的平方差求和，假设有 $m$ 个样本，线性回归的损失函数如下，

J(θ)=12m∑i=1m(hθ(x(i))−y(i))2        (4)J(\theta) = \frac{1}{2m} \sum^m_{i=1} (h_{\theta}(x^{(i)}) - y^{(i)})^2 \ \ \ \ \ \ \ \ (4)

其梯度下降算法公式为：

θj=θj−α1m[∑i=1m(hθ(x(i)−y(i))xj(i)]        (5)\theta_j = \theta_j - \alpha \frac{1}{m}[\sum_{i=1}^m(h_{\theta}(x^{(i)}-y^{(i)})x_j^{(i)}] \ \ \ \ \ \ \ \ (5)

加入$L2$正则化后，其损失函数为

J(θ)=12∑i=1m((hθ(x(i))−y(i))2+λ∑i=1mθj2)        (6)J(\theta) = \frac{1}{2}\sum^m_{i=1}((h_{\theta}(x^{(i)}) - y^{(i)})^2 + \lambda\sum^m_{i=1}\theta_j^2) \ \ \ \ \ \ \ \ (6)

其梯度下降算法公式为：

θj=θj−(α1m[∑i=1m(hθ(x(i)−y(i))xj(i)]+λθj)=θj(1−αλm)−(α1m∑i=1m(hθ(x(i)−y(i))xj(i))        (7)\theta_j = \theta_j - (\alpha \frac{1}{m}[\sum_{i=1}^m(h_{\theta}(x^{(i)}-y^{(i)})x_j^{(i)}] + \lambda \theta_j)=\theta_j(1-\alpha\frac{\lambda}{m}) - (\alpha \frac{1}{m}\sum_{i=1}^m(h_{\theta}(x^{(i)}-y^{(i)})x_j^{(i)}) \ \ \ \ \ \ \ \ (7)

可以看到，由于学习率 $\alpha > 0, \lambda >0$，且这两个值一般都是很小的正数，所以 $0< 1-\alpha\frac{\lambda}{m} < 1$，所以每次 $\theta$ 在更新的时候都会减小，$\lambda$ 越大，衰减的越快，这也是L2正则化可以获得更小的权重值的原因。

正如在线性回归中的应用，$L2$正则化就是在损失函数中加入一个$L2$范数和一个超参数$\lambda$，$L2$范数用 $||w||^2$ 这种符号表示，它的意思是对于向量 $w$ 中的各个数先求平方再加和。线性回归中加入的对于 $\theta_j$ 求平方和就是一个L2范数。超参数$\lambda$ 则用于控制参数惩罚的程度。

我们在举个例子，来展示$L2$正则化如何解决过拟合的现象

来源：吴恩达机器学习课程

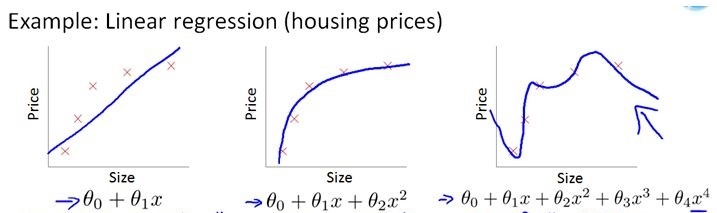
将上述公式分为两部分，左边部分即为原始的损失函数，右边部分为$L2$正则化项（注意：正则化项中不包含$\theta_0$）。$\lambda$ 为超参数，是人为设定的。为了最小化整个损失函数，那么就要减小 $\theta_1$ ~ $\theta_n$ 的值。对于上图中的那种过拟合状态，加入正则项后，$\theta_1$ ~ $\theta_n$减小，也就是使得权重衰减，这样就会降低高阶项对于整个函数的影响，使得估计函数变得比较平滑。

可以想象一种极端的情况，如果$\lambda$ 为无穷大，那么 $\theta_1$ ~ $\theta_n$ 趋近于0，那么整个式子就只剩一个$\theta_0$，为一条和y轴垂直的直线，这种状态为严重的欠拟合状态。可以看到，当$\lambda$为0时，即为原来的状态，此时过拟合。所以会有一个恰当的$\lambda$使得模型处于既不过拟合又不欠拟合的状态。

在未加入$L2$正则化发生过拟合时，拟合函数需要顾忌每一个点，最终形成的拟合函数波动很大，在某些很小的区间里，函数值的变化很剧烈，也就是某些 $w$ 值非常大。为此，$L2$ 正则化的加入惩罚了权重变大的趋势,逼迫所有 $w$ 尽可能趋向零但不为零（$L2$正则化的导数趋于零），导致权重较为平滑。

3. 直观理解为什么$L1$正则更稀疏，$L2$正则权重接近于0.

假设只有一个参数为$w$，损失函数为$L(w)$，分别加上$L1$正则项和$L2$正则项后有：

JL1(w)=L(w)+λ∣w∣JL2(w)=L(w)+λw2J_{L1}(w)=L(w) +\lambda|w| \\ J_{L2}(w)=L(w)+\lambda w^{2}

这里，假设$L(w)$在0处的导数值为$d_{0}$，即：

∂L(w)∂w∣w=0=d0\left.\frac{\partial L(w)}{\partial w}\right|_{w=0}=d_{0}

这时，可以推导使用$L1$正则和$L2$正则时的导数。

当引入$L2$正则项，在$0$处的导数：$\left.\frac{\partial J_{L 2}(w)}{\partial w}\right|{w=0}=d{0}+2 \times \lambda \times w=d_{0}$

引入$L1$正则项，在$0$处的导数：

∂JL1(w)∂w∣w=0−=d0−λ∂JL1(w)∂w∣w=0+=d0+λ\begin{array}{l} \left.\frac{\partial J_{L 1}(w)}{\partial w}\right|_{w=0^{-}}=d_{0}-\lambda \\ \left.\frac{\partial J_{L 1}(w)}{\partial w}\right|_{w=0^{+}}=d_{0}+\lambda \end{array}

可见，引入$L2$正则时，损失函数在0处的导数仍是$d_{0}$ ，无变化。

而引入$L1$正则后，损失函数在$0$处的导数有一个突变。从$d_{0}-\lambda$到$d_{0}+\lambda$。若$d_{0}-\lambda$与$d_{0}+\lambda$异号，则在$0$处会是一个极小值点。因此，优化时，很可能优化到该极小值点上，即$w=0$处。

当然，这里只解释了有一个参数的情况，如果有更多的参数，也是类似的。因此，用L1正则更容易产生稀疏解。

4. 从先验概率分布来了解，为何L1正则更加稀疏？

假设，我们的数据数据是稀疏的,不妨就认为它来自某种$laplace$分布。其中$laplace$的概率密度函数图像如下图所示：

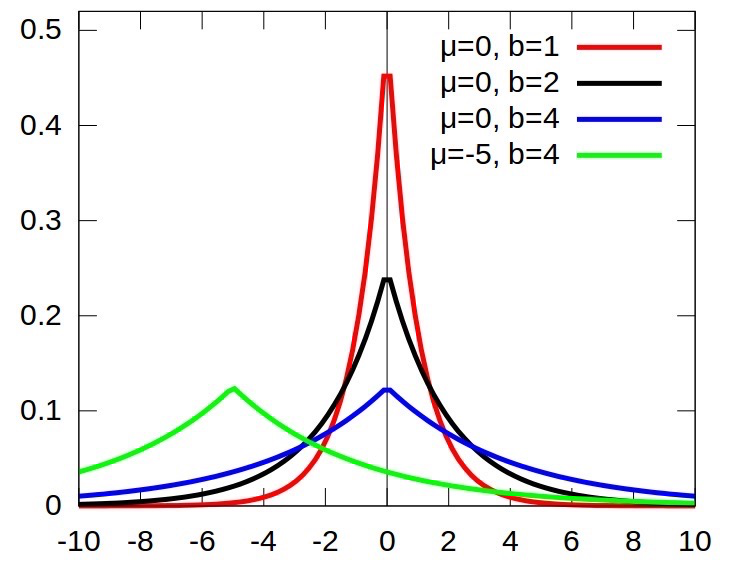
再看看$laplace$分布的概率密度函数:

f(x∣μ,b)=12bexp⁡(−∣x−μ∣b)f(x \mid \mu, b)=\frac{1}{2 b} \exp \left(-\frac{|x-\mu|}{b}\right)

如果取对数,剩下的是一个一次项$|x-u|$,这就是$L1$范式。所以用$L1$范式去正则,就假定了你的数据是稀疏的$laplace$分布。

5. 总结

  • $L1$正则化项是模型各个参数的绝对值之和。$L2$正则化项是模型各个参数的平方和的开方值。

  • $L1$正则化可以使部分权重为$0$，产生稀疏权值矩阵，即产生一个稀疏模型，可以用于特征选择；一定程度上，$L1$也可以防止过拟合，当$L1$的正则化系数很小时，得到的最优解会很小，可以达到和$L2$正则化类似的效果。

  • $L2$正则化通过权重衰减，可以使所有的权重趋向于$0$，但不为$0$，导致模型权重参数较小且较为平滑，防止模型过拟合（$overfitting$）；

  • $L2$正则化的效果是对原最优解的每个元素进行不同比例的放缩；$L1$正则化则会使原最优解的元素产生不同量的偏移，并使某些元素为$0$，从而产生稀疏性。

参考

  1. https://www.cnblogs.com/zingp/p/10375691.html

  2. https://www.jianshu.com/p/27ac92472205

  3. https://www.cnblogs.com/heguanyou/p/7582578.html

  4. https://blog.csdn.net/jinping_shi/article/details/52433975

  5. https://blog.csdn.net/b876144622/article/details/81276818

有趣的经验分享

Previous手写目标检测与语义分割中的IOUNext面试必考 $NMS$汇总

Last updated