enlarge_bs

阅读原文

大家好，我是灿视。

这道题是之前在我之前的那个AttackOnAIer上发过的一题，来自群友在商汤面试的真题，今天重新梳理下，供大家参考。

问： 在Backbone不变的情况下，若显存有限，如何增大训练时的batchsize？

现在给出一些回答，供各位参考哈～ 如果各位有别的想法，可以在留言区留言哈！

使用Trick，节省显寸

  • 使用inplace操作，比如relu激活函数，我们可以使用inplace=True

  • 每次循环结束时候，我们可以手动删除loss，但是这样的操作，效果有限。

  • 使用float16混合精度计算，据有关人士测试过，使用apex，能够节省将近50%的显存，但是还是要小心mean与sum会溢出的操作。

  • 训练过程中的显存占用包括前向与反向所保存的值，所以在我们不需要bp的forward的时候，我们可以使用torch.no_grad()。

  • torch.cuda.empty_cache() 这是del的进阶版，使用nvidia-smi 会发现显存有明显的变化。但是训练时最大的显存占用似乎没变。大家可以试试。

  • 如使用将batchsize=32这样的操作，分成两份，进行forward，再进行backward，不过这样会影响batchnorm与batchsize相关的层。yolo系列cfg文件里面有一个参数就是将batchsize分成几个sub batchsize的。

  • 使用pooling，减小特征图的size，如使用GAP等来代替FC等。

  • optimizer的变换使用，理论上，显寸占用情况 sgd<momentum<adam，可以从计算公式中看出有额外的中间变量。

从反传角度考虑

  • 《Training Deep Nets with Sublinear Memory Cost》

参考陈天奇老师的文章。在训练的时候，CNN的主要开销来自于储存用于计算 backward 的 activation，一般的 workflow 是这样的：

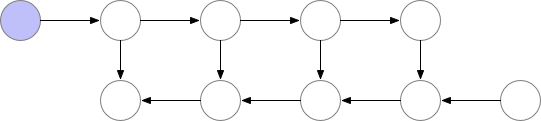
对于一个长度为 N 的 CNN，需要 O(N) 的内存。这篇论文给出了一个思路，每隔 sqrt(N) 个 node 存一个 activation，中需要的时候再算，这样显存就从 O(N) 降到了 O(sqrt(N))。

对于越深的模型，这个方法省的显存就越多，且速度不会明显变慢。其中$pytorch$本身也有$torch.utils.checkpoint$这样的函数实现一样的功能。

补充

对于题目而言，是为了增大$Batch$ $size$。同样，如果显存真的特别有限，我们怎么办呢？

我们也可以将小$batch$ $size$的数据达到大$batch$ $size$的效果。

举个例子，假设由于显存限制$DataLoader$的$batch$ $size$只能设为4，想要通过梯度累积实现$batch$ $size$等于16，这需要进行四次迭代，每次迭代的$loss$除以4，这里给一个参考代码：


for i,(images,target) in enumerate(train_loader):
    # 1. input output
    images = images.cuda(non_blocking=True)
    target = torch.from_numpy(np.array(target)).float().cuda(non_blocking=True)
    outputs = model(images)
    loss = criterion(outputs,target)

    # 2.1 loss regularization
    loss = loss/accumulation_steps   
    # 2.2 back propagation
    loss.backward()
    # 3. update parameters of net
    if((i+1)%accumulation_steps)==0:
        # optimizer the net
        optimizer.step()        # update parameters of net
        optimizer.zero_grad()   # reset gradient

首先，获取$loss$, 在计算当前梯度，不过我们暂先不清空梯度，是梯度加在已有梯度上。当梯度累加到了一定次数之后，使用$optimizer.step()$将累计的梯度来更新参数。

一定条件下，$batch$ $size$越大训练效果越好，梯度累加则实现了$batch$ $size$的变相扩大。但，增大$bs$的同时，需要我们适当方法学习率。

不过使用$accumulation_step=8$的效果是不如真实的$batch$ $size$放大8倍。因为增大$8$倍$batch$ $size$的图片，其$sunning_mean$与$running_var$更加准确。

Previousdropout_2Nextim2col

Last updated