CV中的Attention

如公式与图片显示不好，点此阅读原文

1. 直观理解Attention

想象一个场景，你在开车（真开车！握方向盘的那种！非彼开车！），这时候下雨了，如下图。

那你想要看清楚马路，你需要怎么办呢？dei!很聪明，打开雨刮器就好！

那我们可以把这个雨刮器刮雨的动作，就是寻找Attention区域的过程！嗯！掌声鼓励下自己，你已经理解了Attention机制！

2. 再看Attention机制

首先，我们引入一个概念叫做$<Key, Value>$，键值对。如在$Python$中的$Dict$类型的数据就是键值对存储的，相当于一对一的概念 (如，我们婚姻法，合法夫妻就是一对一)。

dict = {'name' : 'canshi'}   #name为canshi

回忆一下，在中学时期，我们学的眼睛成像！一张图在眼睛中是一个倒立的缩放图片，然后大脑把它正过来了。我们开始进行建模，假设这个自然界存在的东西就是Key，同时也叫Value。

套下公式，当下雨的时候，冷冷的冰雨在车窗上狠狠的拍！我们把这个整个正在被拍的车窗叫做Key，同时也叫Value。但是我们看不清路呀，我们这时候就想让我们可以分得清路面上的主要信息就好，也不需要边边角角的信息。那么这个时候，雨刮器出场了，我们把它叫做Query! 我们就能得到一个看清主要路面的图片了！

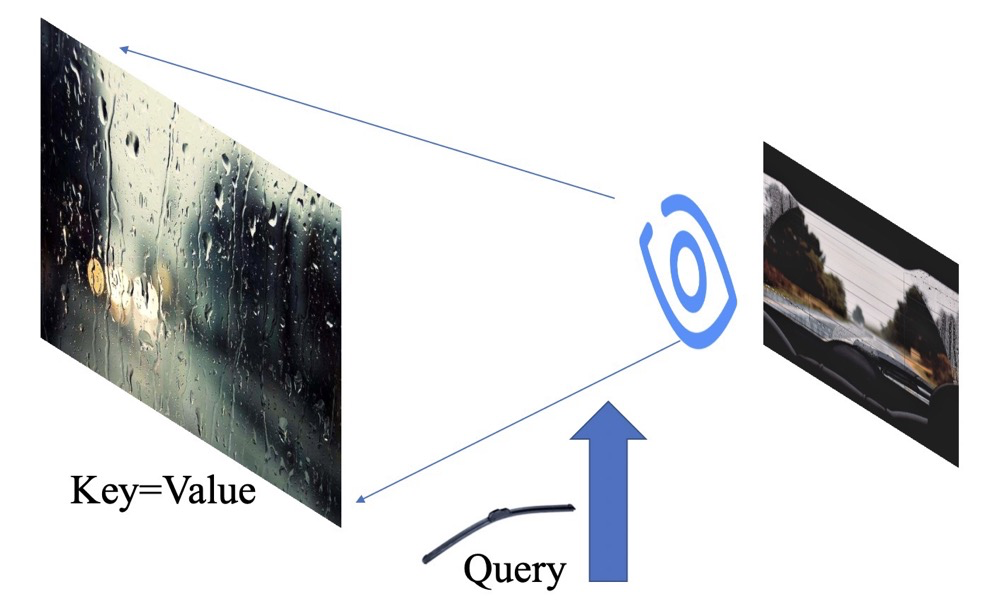
那么到底发生了什么了呢？我来拆开下哈：

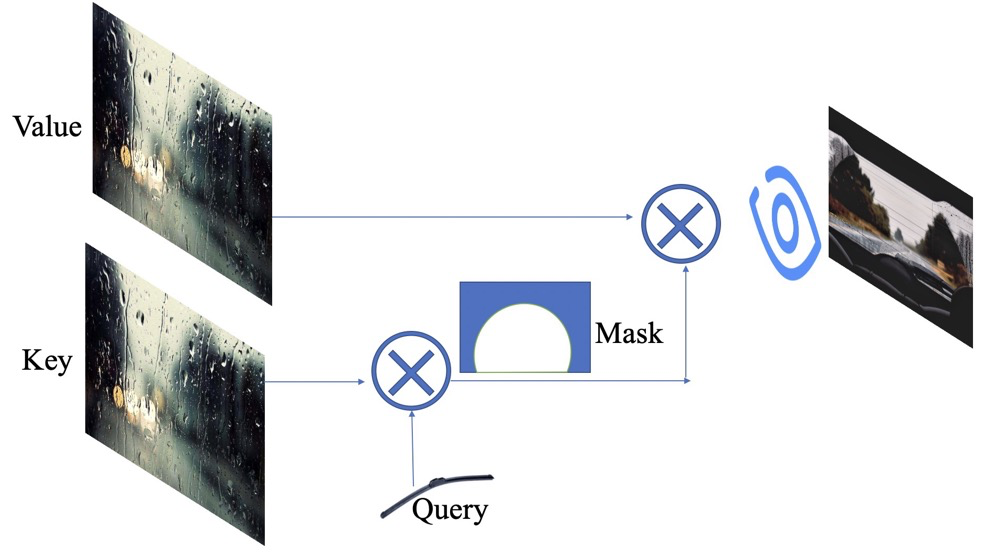
所以，我们通过雨刮器($Query$)来作用于车窗图($Key$), 得到了一个部分干净的图像(类$Mask$，里面的值是0~1),图片中白色区域表示擦干净了，其它部分表示不用管。再用这个生成的$Mask$ 与$Value$ 图做乘积，得到部分干净的生成图像，显示在我们的大脑中。

因此，我们会看到一些说$Attention$的博客会有下面的图：

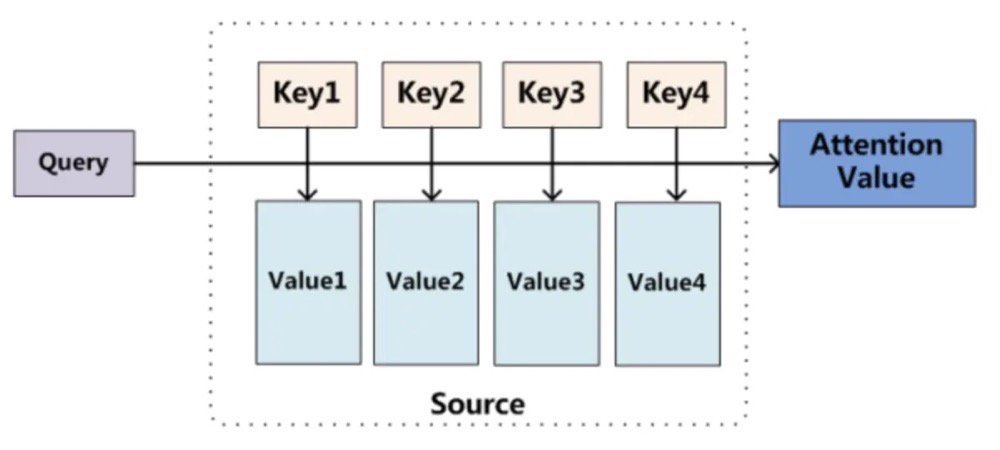
这张图主要是针对于机器翻译中用的，在翻译的时候，每一个输出$Query$需要于输入$Key$的各个元素计算相似度，再与$Value$ 进行加权求和～

对于$CV$领域中，我们一般都是用矩阵运算了，不像$NLP$中的任务，需要按照时刻进行，$CV$中的任务，就是一个矩阵运算，一把梭就完事儿了。

比如这个雨刮器刮水的过程。我们把原先带是雨水的车窗记作$S$，雨刮器来刮雨就是$Q$，我们使用相似度来代替刮水的过程，得到一个$Mask$。再用$Mask$与原图像$V$通过计算，得到最后的图像。

因此，用公式来概括性地描述就是：

 Attention ( Q, S )= Similarity ( Q,K)∗ V \text { Attention }(\text { Q, S })= \text { Similarity }\left(\text { Q}, K \right) * \text { V }

划重点，不同的车有不同的雨刷来进行刮雨，同样，我们有不同的方法来衡量相似度，这里我们主要有以下几种方案来衡量相似度：

 点积: Similarity ( Q ,K)= Q ⋅K Cosine相似性:  Similarity ( Q ,K)= Q ⋅K∣ Q ∣⋅∣K∣MLP 网络: Similarity ( Q, K)=MLP( Q ,K)\begin{array}{r} \text { 点积: Similarity }\left(\text { Q }, \mathrm{K}\right)=\text { Q } \cdot \mathrm{K} \\ \text { Cosine相似性: } \text { Similarity }\left(\text { Q }, K\right)=\frac{\text { Q } \cdot K}{\mid \text { Q }|\cdot| K \mid} \\ M L P \text { 网络: Similarity }\left(\text { Q, } K \right)=M L P\left(\text { Q }, K\right) \end{array}

当有了相似度之后，我们需要对其进行归一化，将原始计算分值整理成所有元素权重之和为1的概率分布，越重要的部分，越大！越不重要的部分，越小。我们采用$Softmax$为主，当然也有一些使用$Sigmoid$这样来进行运算，都是ok的～

因此，这个权重$Mask$的值可以这么计算：

Mask=softmax⁡(QKTdk)Mask = \operatorname{softmax}\left(\frac{Q K^{T}}{\sqrt{d_{k}}}\right)

其中$\sqrt{d_{k}}$表明将数据进行下缩放，防止过大了。

最后就是得到$Attention$的输出了：

 Attention (Q,K,V)=Mask∗V\text { Attention }(Q, K, V)=Mask * V

因此，像戴眼镜，也是一种$Attention$,。对于眼睛里的区域进行进行聚焦，而除此之外的区域，就无所谓了。不需要进行额外处理了。

3. 大脑中的Attention机制

人在成长过程中，可能每一个阶段都会对大脑进行训练，让我们在大自然界中快速得到我们想要的信息。当前大数据时代，那么多图片视频，我们需要快速浏览得到信息，比如下面的图：

我可能一开始就会注意到这个大衣是很好的款式，这个红色的小包也不错，当然每个人从小到大用来训练的数据集是不一样的，我也不知道你们第一眼看到的是啥！毕竟这个注意力$Mask$矩阵，需要海量的数据来进行测试。

哦？还跟我拗？那你也来试试下面的挑战？

原视频来自 B站，非P站！

3. CV中常用的Attention

1. Non-local Attention

通过上面的例子，我们就明白了，原来$Attention$本质就是在一个维度上进行计算权重矩阵。这个维度如果是空间，那么就是Spatial Attention, 如果是通道这个维度，那么就是Channel Attention。所以，如果以后你投稿的时候，再说你$Novelty$不够，我们就可以搭积木搭出来一个$Attention$模块呀！

这里我们使用$Non-Local$ $Block$来讲解下，常用在$CV$领域中的Attention。

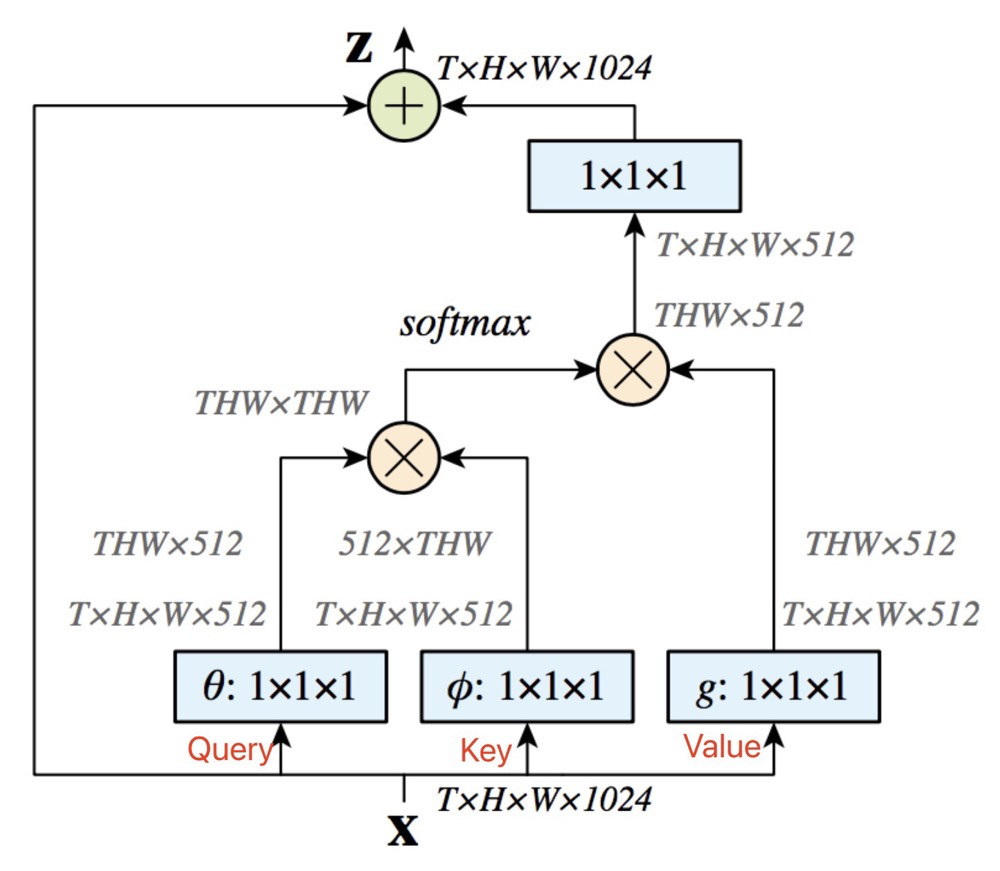
输入特征$x$，通过$1 * 1$卷积来得到$Key,Query,Value$，这里的三个矩阵是不同的，因此上文中是**假设 **相同。

其中代码如下：

class Self_Attn(nn.Module):
    """ Self attention Layer"""
    def __init__(self,in_dim,activation):
        super(Self_Attn,self).__init__()
        self.chanel_in = in_dim
        self.activation = activation
        
        self.query_conv = nn.Conv2d(in_channels = in_dim , out_channels = in_dim//8 , kernel_size= 1)
        self.key_conv = nn.Conv2d(in_channels = in_dim , out_channels = in_dim//8 , kernel_size= 1)
        self.value_conv = nn.Conv2d(in_channels = in_dim , out_channels = in_dim , kernel_size= 1)
        self.gamma = nn.Parameter(torch.zeros(1))

        self.softmax  = nn.Softmax(dim=-1) #
    def forward(self,x):
        """
            inputs :
                x : input feature maps( B X C X W X H)
            returns :
                out : self attention value + input feature 
                attention: B X N X N (N is Width*Height)
        """
        m_batchsize,C,width ,height = x.size()
        proj_query  = self.query_conv(x).view(m_batchsize,-1,width*height).permute(0,2,1) # B X CX(N)
        proj_key =  self.key_conv(x).view(m_batchsize,-1,width*height) # B X C x (*W*H)
        energy =  torch.bmm(proj_query,proj_key) # transpose check
        attention = self.softmax(energy) # BX (N) X (N) 
        proj_value = self.value_conv(x).view(m_batchsize,-1,width*height) # B X C X N

        out = torch.bmm(proj_value,attention.permute(0,2,1) )
        out = out.view(m_batchsize,C,width,height)
        
        out = self.gamma*out + x
        return out,attention

代码看上去还是比较容易懂得，主要就是$torch.bmm()$函数，它可以将纬度为$B * N * C$矩阵与$B * C N$的矩阵相乘的到$BN*N$的矩阵。再使用$Softmax$来得到归一化之后的矩阵，结合残差，得到最后的输出！

2. CBAM

$CBAM$由$Channel$ $Attention$与$Spatial$ $Attention$组合而成。

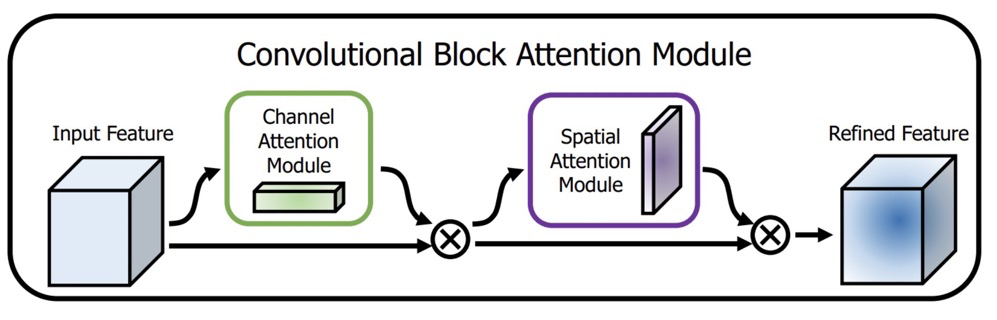
其中的$Channel$ $Attention$ 模块，主要是从C x H x w 的纬度，学习到一个C x 1 x 1的权重矩阵。

论文中的图如下：

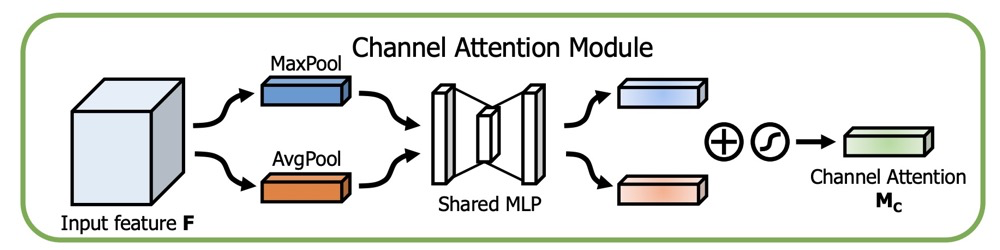
代码示例如下：

class ChannelAttentionModule(nn.Module):
   def __init__(self, channel, reduction=16):
       super(ChannelAttentionModule, self).__init__()
       mid_channel = channel // reduction
       self.avg_pool = nn.AdaptiveAvgPool2d(1)
       self.max_pool = nn.AdaptiveMaxPool2d(1)

       self.shared_MLP = nn.Sequential(
           nn.Linear(in_features=channel, out_features=mid_channel),
           nn.ReLU(inplace=True),
           nn.Linear(in_features=mid_channel, out_features=channel)
       )
       self.sigmoid = nn.Sigmoid()

   def forward(self, x):
       avgout = self.shared_MLP(self.avg_pool(x).view(x.size(0),-1)).unsqueeze(2).unsqueeze(3)
       maxout = self.shared_MLP(self.max_pool(x).view(x.size(0),-1)).unsqueeze(2).unsqueeze(3)
       return self.sigmoid(avgout + maxout)

当然，我们可以使用$Query,Value, Key$的形式来对它进行修改成一个统一架构，只要我们可以学习到一个在通道纬度上的分布矩阵就好。

如下方伪代码，$key, value, query$ 均为$1 * 1$卷积生成。

# key: (N, C, H, W)
# query: (N, C, H, W)
# value: (N, C, H, W)
key = key_conv(x)
query = query_conv(x)
value = value_conv(x)

mask = nn.softmax(torch.bmm(key.view(N, C, H*W), query.view(N, C, H*W).permute(0,2,1)))
out = (mask * value.view(N, C, H*W)).view(N, C, H, W)

对于$Spatial$ $Attention$，如图所示：

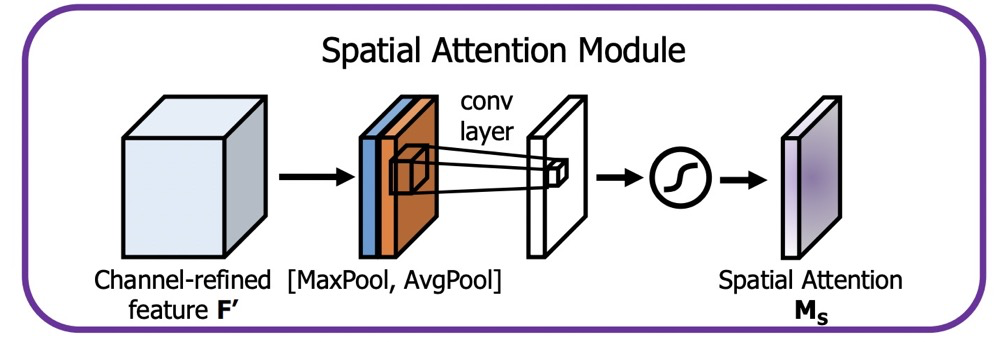
参考代码如下：

class SpatialAttentionModule(nn.Module):
    def __init__(self):
        super(SpatialAttentionModule, self).__init__()
        self.conv2d = nn.Conv2d(in_channels=2, out_channels=1, kernel_size=7, stride=1, padding=3)
        self.sigmoid = nn.Sigmoid()

    def forward(self, x):
        avgout = torch.mean(x, dim=1, keepdim=True)
        maxout, _ = torch.max(x, dim=1, keepdim=True)
        out = torch.cat([avgout, maxout], dim=1)
        out = self.sigmoid(self.conv2d(out))
        return out

采用$Query, Key, Value$的框架来进行改写：

key = key_conv(x)
query = query_conv(x)
value = value_conv(x)

b, c, h, w = t.size()
query = query.view(b, c, -1).permute(0, 2, 1)
key = key.view(b, c, -1)
value = value.view(b, c, -1).permute(0, 2, 1)

att = torch.bmm(query, key)

if self.use_scale:
		att = att.div(c**0.5)

att = self.softmax(att)
x = torch.bmm(att, value)

x = x.permute(0, 2, 1)
x = x.contiguous()
x = x.view(b, c, h, w)

3. cgnl

论文分析了下如$Spatial$ $Attention$与$Channel$ $Attention$均不能很好的描述特征之间的关系，这里比较极端得生成了N * 1 * 1 * 1的$MASK$.

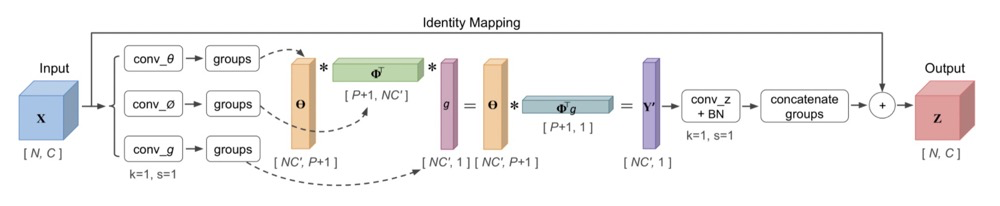
主要关于$Attention$计算的部分代码：

def kernel(self, t, p, g, b, c, h, w):
        """The linear kernel (dot production).
        Args:
            t: output of conv theata
            p: output of conv phi
            g: output of conv g
            b: batch size
            c: channels number
            h: height of featuremaps
            w: width of featuremaps
        """
        t = t.view(b, 1, c * h * w)
        p = p.view(b, 1, c * h * w)
        g = g.view(b, c * h * w, 1)

        att = torch.bmm(p, g)

        if self.use_scale:
            att = att.div((c*h*w)**0.5)

        x = torch.bmm(att, t)
        x = x.view(b, c, h, w)

        return x

4. Cross-layer non-local

论文中分析了，同样的层之间进行$Attention$计算，感受野重复，会造成冗余，如左边的部分图，而右边的图表示不同层间的感受野不同，计算全局$Attention$也会关注到更多的区域。

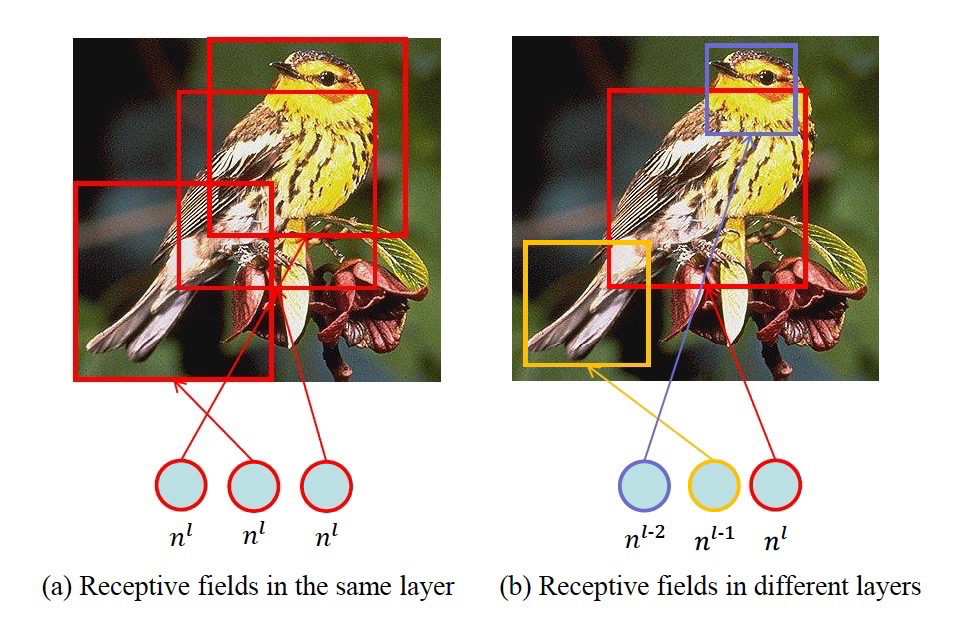
这里采用跨层之间的$Attention$生成。

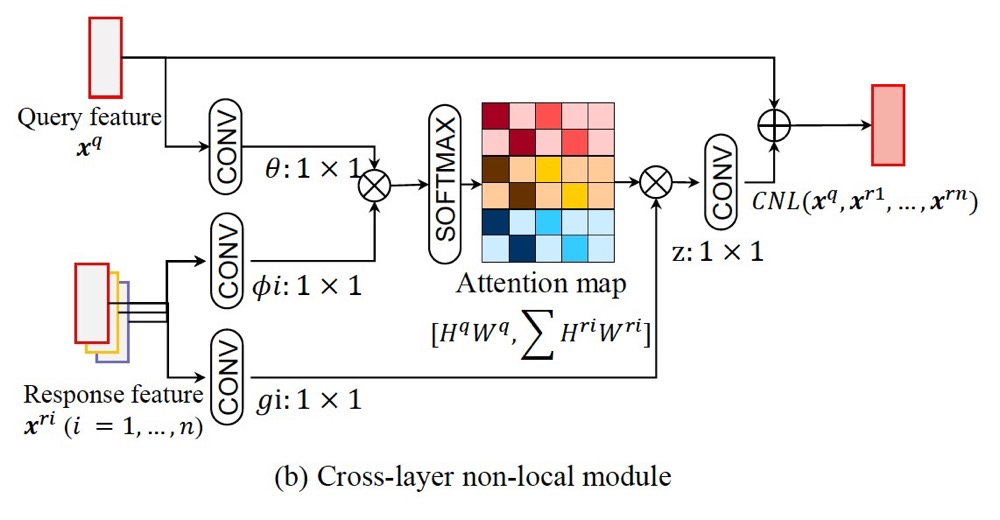
代码部分比较有意思：

# query : N, C1, H1, W1
# key: N, C2, H2, W2
# value: N, C2, H2, W2
# 首先，需要使用1 x 1 卷积，使得通道数相同
q = query_conv(query) # N, C, H1, W1
k = key_conv(key) # N, C, H2, W2
v = value_conv(value) # N, C, H2, W2
att = nn.softmax(torch.bmm(q.view(N, C, H1*W1).permute(0, 1, 2), k.view(N, C, H2 * W2))) # (N, H1*W1, H2*W2)
out = att * value.view(N, C2, H2*W2).permute(0, 1, 2) #(N, H1 * W1, C)
out = out.view(N, C1, H1, W1)

4. 小结

$Attention$是一个比较适合用来写文章的知识点，算是一个$Novelty$的点。目前针对$CV$中的$Attention$差不多可以概括为这些，后面会继续补充，欢迎各位关注！

Previous1x1Next介绍下DenseNet

Last updated