激活函数

阅读原文

一文梳理常见的激活函数

1. 为什么要有激活函数

若网络中不用激活函数，那么每一层的输出都是输入的线性组合。无论神经网络有多少层，网络的输出都是输入的线性组合，这种网络就是原始的感知机（$Perceptron$）。若网络没有激活函数，则每层就相当于矩阵相乘，深层神经网络，无非是多矩阵相乘。

激活函数给神经元引入了非线性因素，使得神经网络可以任意逼近任何非线性函数，这样神经网络就可以应用到众多的非线性模型中。网络使用非线性激活函数后，可以增加神经网络模型的非线性因素，网络可以更加强大，表示输入输出之间非线性的复杂的任意函数映射。

网络的输出层可能会使用线性激活函数，但隐含层一般都是使用非线性激活函数。

2. 非零均值的问题（non-zero-centered）

部分激活函数是非零均值的，如$ReLU$, $Sigmoid$等激活函数，他会造成网络收敛很慢。我们可以简单看下表示式：$f=(w_{i} x_{i}+b)$，其中$x_{i}$为$sigmoid$函数的输出。那么，在计算损失函数后，需要进行反向传播更新该权重$w_{i}$。这时候，对$w_{i}$进行求导，是直接与$x_{i}$相关的，而因为$x_{i}$是大于$0$的值，所以这时候的梯度方向就会完全取决于$\frac{dL}{df}$。这时候若$\frac{dL}{df}$恒正或者恒为负，那么就会出现$zig-zagging$ $dynamics$的问题,使得网络收敛变慢。

其中$zig-zagging$ 的图像就如下面图像：

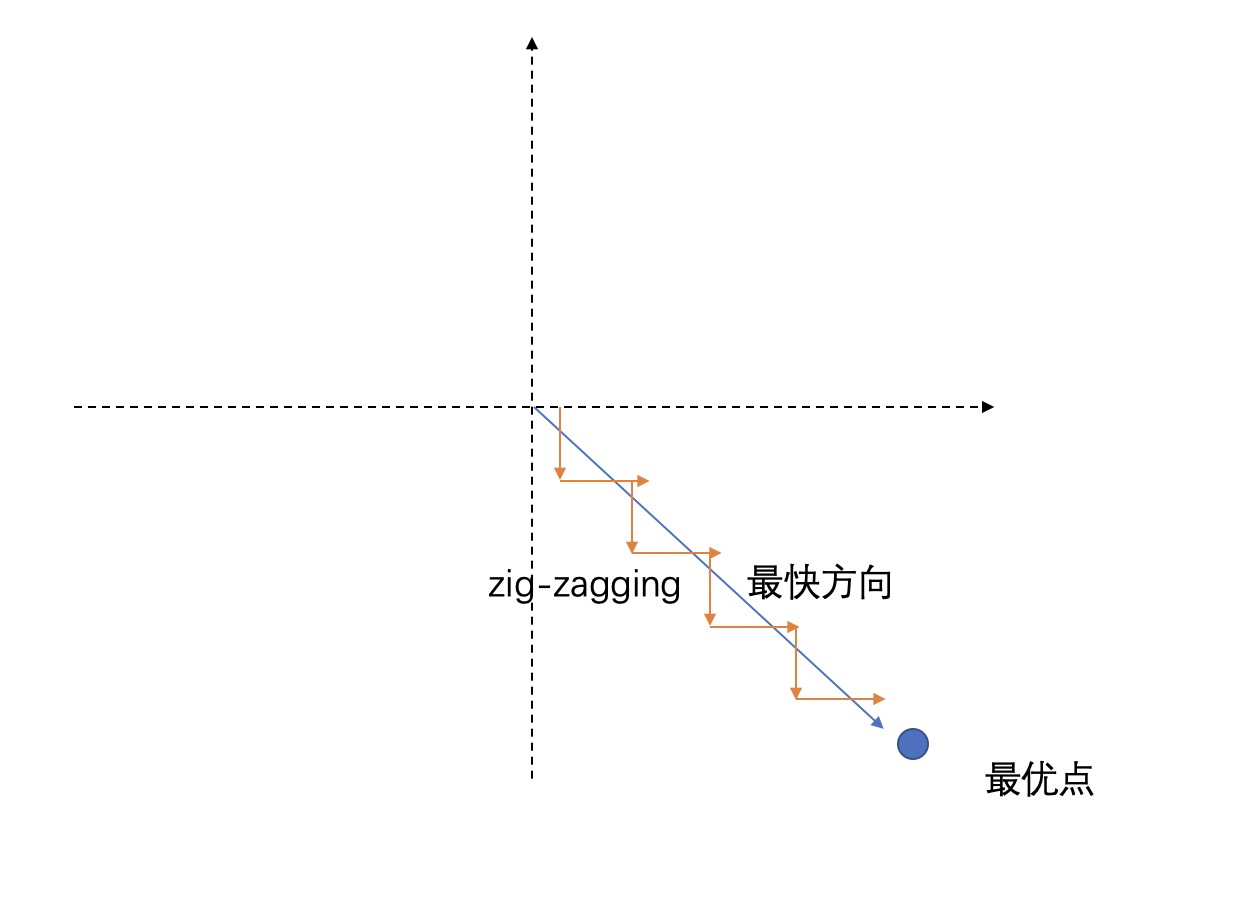
下面开始我们介绍下常用的激活函数，其中对于部分激活函数，画图都是采用Pytorch中Functional的默认参数来进行绘制的。

1. Sigmoid激活函数

sigmoid函数公式如下:

f(z)=11+exp⁡(−z)f(z)=\frac{1}{1+\exp (-z)}

$Sigmoid$函数也叫$Logistic$函数，用于用于隐层神经元输出，取值范围为$(0,1)$，它可以将一个实数映射到$(0,1)$ 的区间，可以用来做二分类或者生成$Attention$ $ Mask$。在特征相差比较复杂或是相差不是特别大时效果比较好。

$sigmoid$ 激活函数的缺点有：

  • 激活函数计算量大，反向传播求误差梯度时，求导涉及除法；

  • 反向传播时，很容易就会出现梯度消失的情况，从而无法完成深层网络的训练；

  • $Sigmoid$ 是非零均值的函数，收敛缓慢。

  • $Sigmoid$函数运算量大。如我们用$FLOPs$(每秒浮点操作次数)来衡量模型的计算量指标。则$ReLU$运算量是1 $FLOPs$。那么Sigmoid包括了减、取幂、加、除共4 $FLOPs$.

$sigmoid$ 激活函数出现梯度消失的原因如下：

反向传播算法中，要对激活函数求导，$sigmoid$ 的导数表达式为：

ϕ′(x)=ϕ(x)(1−ϕ(x))\phi^{\prime}(x)=\phi(x)(1-\phi(x))

$sigmoid$ 激活函数原函数及导数图形如下：由图可知，导数从0 开始很快就又趋近于0 了，易造成“梯度消失”现象。

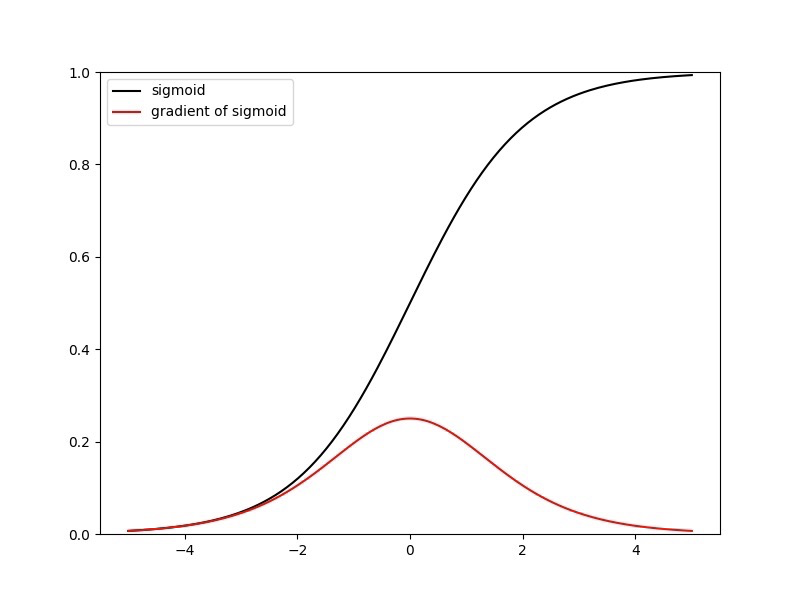
2. TanH激活函数

$TanH$ 激活函数的公式如下，也称为双切正切函数，取值范围为[-1,1]。

tanh⁡(x)=2sigmoid⁡(2x)−1f(z)=tanh⁡(z)=ez−e−zez+e−z\begin{array}{l} \tanh (x)=2 \operatorname{sigmoid}(2 x)-1 \\ f(z)=\tanh (z)=\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}} \end{array}

而$Tanh$函数的反传公式为：

g′(z)=(ez−e−zez+e−z)′=4(ez+e−z)2=1−g(z)2\begin{aligned} g^{\prime}(z) &=\left(\frac{e^{z}-e^{-z}}{e^{z}+e^{-z}}\right)^{\prime} \\ &=\frac{4}{\left(e^{z}+e^{-z}\right)^{2}} \\ &=1-g(z)^{2} \end{aligned}

$TanH$函数的缺点同$sigmoid$函数的缺点类似。当 z 很大或很小时，𝑔′(𝑧) 接近于 0 ，会导致梯度很小，权重更新非常缓慢，即梯度消失问题。从下面的图像也能看出来，靠近图像两端越平缓，梯度越小。

$TanH$ 激活函数函数图像如图所示。

$Tanh$ 在特征相差明显时的效果会相对更好，在循环过程中会不断扩大特征效果。与$sigmoid$ 的区别是，$tanh$ 是$0$ 均值的，因此实际应用中$tanh$ 会比$sigmoid$ 更好，不过需要具体尝试。

3. ReLU激活函数

$ReLU$ (Rectified Liner Unit)激活函数主要用于隐层神经元输出，公式为$f(x)=max(0,x)$，函数图像与其求导的导数图像如图所示:

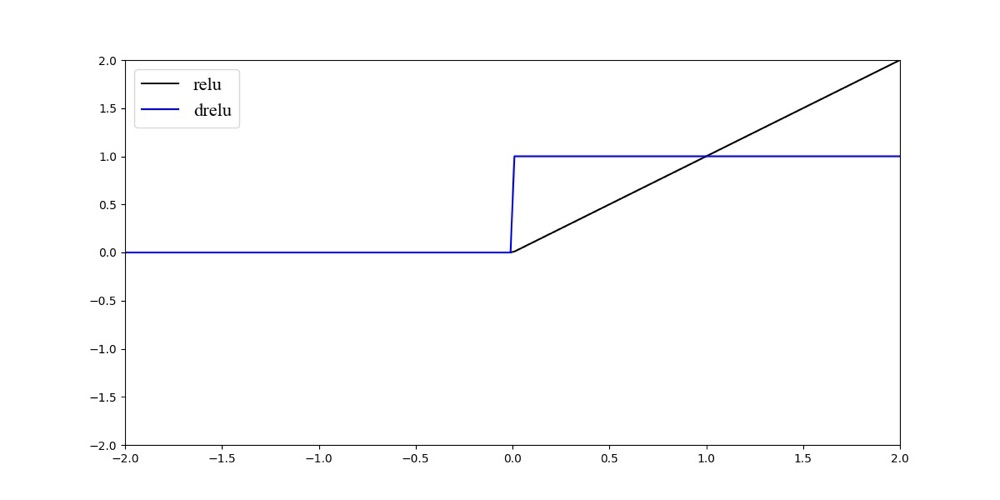
  • $ReLU$ 激活函数的特点是：输入信号小于时，输出都是0，输入信号大于0时，输出等于输入。

  • $ReLU$ 的优点是使用$ReLU$ 得到的$SGD$ 的收敛速度会比使用$sigmoid/tanh$的$SGD$ 快很多。

  • $ReLU$ 的缺点是神经网络训练的时候很“脆弱”，很容易就会出现神经元死亡。

    例如，一个非常大的梯度流过一个$ReLU$ 神经元，更新过参数之后，这个神经元再也不会对任何数据有激活现象了，那么这个神经元的梯度就永远都会是$0$。（Dead ReLU Problem）。

  • 非零均值，所以一般$ReLU$后会加$BN$。

4. Softmax 激活函数

多用于多分类神经网络输出，公式为：

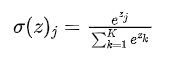
主要用于分类最后归一化到$[0,1]$ ，$j \in [1, K]$。当然也与$Sigmoid$一样，可以用在attention之中，学习到权重的矩阵。

5. Softplus激活函数

公式如下：

y=log⁡(1+ex)y=\log \left(1+e^{x}\right)

将$ReLU$与$Softplus$放在一起对比的话，则如图像所示：

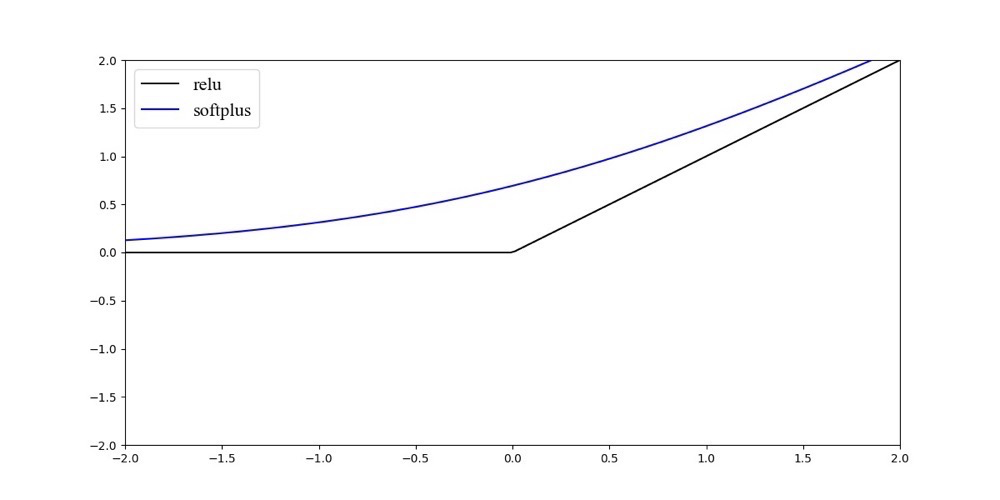
可以看到，$softplus$可以看作是$ReLU$的平滑。其中，加了$1$是为了保证非负性。$Softplus$可以看作是强制非负校正函数$max(0,x)$平滑版本。

6. Mish激活函数

$Mish$函数的公式如下：

 Mish =x∗tanh⁡(ln⁡(1+ex))\text { Mish }=x * \tanh \left(\ln \left(1+e^{x}\right)\right)

在$Pytorch$中 $Mish$激活函数代码如下：

x = x * (torch.tanh(F.softplus(x)))

函数图像如图所示：

$Mish$函数,以上无边界(即正值可以达到任何高度)避免了由于封顶而导致的饱和。理论上对负值的轻微允许允许更好的梯度流，而不是像$ReLU$中那样的硬零边界。

最后，可能也是最重要的，平滑的激活函数允许更好的信息深入神经网络，从而得到更好的准确性和泛化。

不过我 之前亲自训过$Mish$这个激活函数，$Pytorch$版本的$Mish$很占显存。

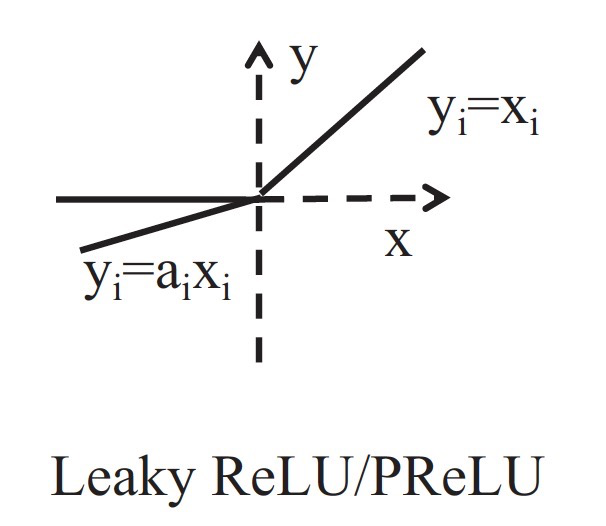
7. Leaky ReLU与PReLU

$Leaky$ $ReLU$的公式如下:

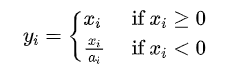
$a_{i}$是一个$(1,+\infty)$区间内的固定参数。与 $ReLU$ 相比 ，$leaky$ $ReLU$ 给所有负值赋予一个非零斜率$a_{i}$。这样保留了一些负轴的值，使得负轴的信息不会全部丢失。

而 $PReLU$可以看作是$Leaky$ $ReLU$的一个变体。在$PReLU$中，负值部分的斜率$a_{i}$是根据网络学习来定的，而非预先定义的。作者称，在$ImageNet$分类（2015，Russakovsky等）上，$PReLU$是超越人类分类水平的关键所在。

如$Leaky$ $ReLU$与$PReLU$主要的特点是：（1）计算简单，有效 （2）比$Sigmoid$与$Tanh$收敛更快 (3) 解决了$Dead$ $ReLU$的问题。

8. RReLU激活函数

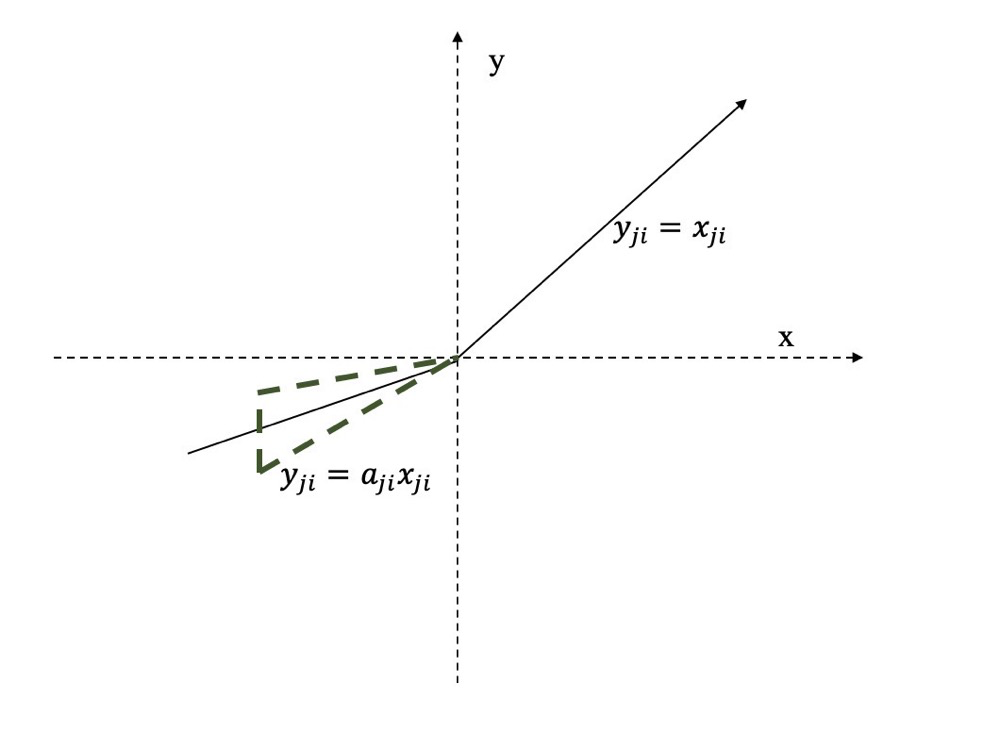
$RReLU$(Randomized leaky rectified linear unit)也是$Leaky$ $ReLU$的一个变体。在$RReLU$中，$a_{ji}$是一个在一个给定的范围内随机抽取的值，这个值在测试环节就会固定下来

$RReLU$的亮点在于，在训练环节中，$a_{ji}$是从一个均匀的分布$U(I,u)$中随机抽取的数值。形式上来说，我们能得到以下结果:

where

aji∼U(l,u),l<u,u∈[0,1)a_{j i} \sim U(l, u), l < u, u \in [0, 1)

该函数的图像如下图所示：

9. ELU激活函数

$ELU$同样是针对$ReLU$的负数部分进行的改进，$ELU$激活函数对$x$小于零的情况采用类似指数计算的方式进行输出：

ELU⁡(x)=max⁡(0,x)+min⁡(0,α∗(exp⁡(x)−1))\operatorname{ELU}(x)=\max (0, x)+\min (0, \alpha *(\exp (x)-1))

或者表达为：

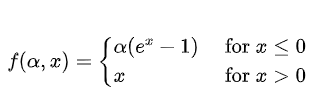
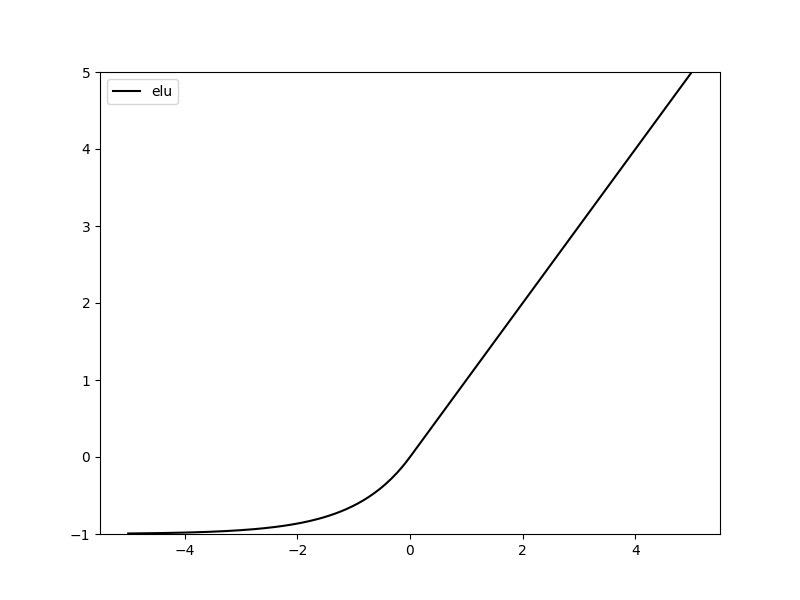
对于$ELU$有这些特点：

  • $ELU$由于其正值特性，可以像$ReLU$,$Leaky$ $ReLU$, $PReLU$一样缓解梯度消失的问题。

  • 相比$ReLU$，$ELU$存在负值，可以将激活单元的输出均值往$0$推近，达到接近$BN$的效果同时减少了计算量。

10. Swish激活函数

激活函数的公式如下：

f(x)=x⋅sigmoid⁡(βx)f(x)=x \cdot \operatorname{sigmoid}(\beta x)

其函数图像如下：

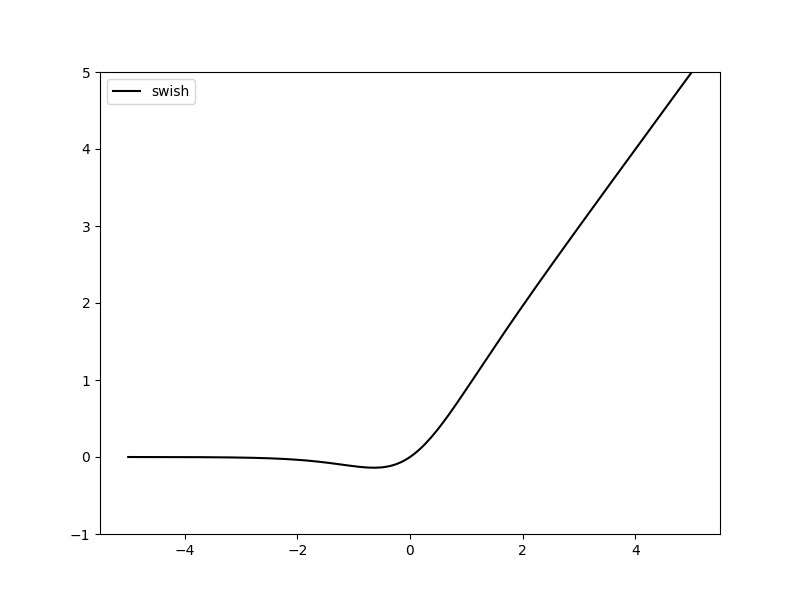
其中，$\beta$是常数或可训练的参数。$Swish$函数具备无上界有下界、平滑、非单调的特性。通过实验证明，对于深层模型， $Swish$的效果是优于$ReLU$的。

当$\beta=0$时，$Swish$激活函数成为线性函数$f(x)=\frac{x}{2}$。 当$\beta \rightarrow \infty, \sigma(x)=(1+\exp (-x))^{-1}$ 为0或1. Swish变为ReLU: $f(x)=2 \max (0, x)$。 以$Swish$函数可以看做是介于线性函数与$ReLU$函数之间的平滑函数.

11. SELU激活函数

$SELU$是给$ELU$乘上系数 $\beta$, 即$ SELU(x)=𝜆⋅ELU(x)$。

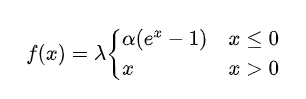
文章中主要证明是当取得$\lambda \approx 1.0507, \alpha \approx 1.6733$时，在网络权重服从标准正态分布的条件下，各层输出的分布会向标准正态分布靠拢，这种"自我标准化"的特性可以避免梯度消失于梯度爆炸，证明过程各位感兴趣的可以去看看90多页的原文。

函数图像如图所示：

12. GELU激活函数

受启发于$Dropout$、$ReLU$等机制的影响，都意在将不重要的信息设置为0。对于输入的值，我们可以理解成是将输入的值乘以了一个0或者1。即对于每一个输入$x$,其服从于标准正态分布$N(0,1)$，它也会乘以一个伯努利分布$Bernoulli(\phi(x))$，其中$\phi(x)=P(x \leq x)$。

$GELU$(Gaussian error linear units)的表达式为$\operatorname{GELU}(x)=x P(X \leq x)=x \Phi(x)$。

而上式函数是无法直接计算的，因此可以使用另外的方式来进行逼近，论文得到的表达式为：$0.5 x\left(1+\tanh \left[\sqrt{2 / \pi}\left(x+0.044715 x^{3}\right)\right]\right)$。或者为$GELU(x)=\frac{x}{1+e^{-1.702 x}}$。

$bert$, $Transformer$中使用的激活函数，作者经过实验证明比$relu$等要好。原点可导，不会有$Dead$ $ReLU$问题。

其函数图像如图所示：

Previous深度学习之权重初始化Next原因

Last updated