我丢！Drop就完事了！（上）

大家好，我是灿视。

今天我们来以Dropout为切入点，汇总下那些各种Drop的操作。本片是上篇，还有续集，欢迎关注我们，追更《百面计算机视觉第三版》哦！

Dropout

目前来说，$Dropout$有两种。第一种就是传统的$Dropout$方案。另一种，就是我们的吴恩达老师所讲的$Inverted$ $Dropout$了。这两种方案本质上没什么区别，在实现的过程中是有区别的，接下来我们会详细进行比较。

这里先给出其数学公式：

$Training$ $Phase$ :

\mathbf{y}=f(\mathbf{W} \mathbf{x}) \circ \mathbf{m}, \quad m_{i} \sim \operatorname{Bernoulli}(p)

$Testing$ $Phase$ :

\mathbf{y}=(1-p) f(\mathbf{W} \mathbf{x})

首先，看下$Dropout$论文中给出的图像，了解下$Dropout$究竟干了个啥。

概括来说：Dropout提供了一种有效地近似组合指数级的不同经典网络架构的方法。

将$Dropout$应用到神经网络中，相当于从该网络中采样一些子网络。这些子网络由所有在$Dropout$操作后存活下来的单元节点组成。如果一个神经网络有$n$个节点，则能够产生$2^{n}$中可能的子网络。在测试阶段，我们不是直接将这些指数级的子网络显式的取平均预测，而是采用一种近似的方法：仅使用单个神经网络，该网络的权重是先前训练的网络权重乘以失活概率$p$。这样做可以使得在训练阶段隐藏层的期望输出（在随机丢弃神经元的分布）同测试阶段是一致的。这样可以使得这$2^{n}$个网络可以共享权重。

$Inverted$ $Dropout$

先看下$Inverted$ $Dropout$的实现代码，假设，我们的输入是$x$，$p$表示随机丢弃的概率, $1-p$表示的是神经元保存的概率。则$Inverted$ $Dropout$的实现过程如下代码所示：

import numpy as np
def dropout(x, p):
    if p < 0. or p >1.
        # 边界条件，在写代码的时候，一定要仔细！！！p为随机丢弃的概率
        raise Exception("The p must be in interval [0, 1]")
    retain_prob =1. -p
    #我们通过binomial函数，生成与x一样的维数向量。
    # binomial函数就像抛硬币一样，每个神经元扔一次，所以n=1
    # sample为生成的一个0与1构成的mask,0表示抛弃，1表示保留
    sample =np.random.binomial(n=1, p=retain_prob, size=x.shape)
    x *= sample # 与0相乘，表示将该神经元Drop掉
    x /= retain_prob
    return x

这里解释下，为什么在后面还需要进行 x/=retain_prob 的操作？

假设该层是输入，它的期望是$a$，在不使用$Dropout$的时候，它的期望依旧是$a$。如果该层进行了$Dropout$, 相当于有$p$的概率被丢弃，$1-p$的概率被保留，则此层的期望为$(1-p) * a * 1+ p * a * 0 = (1-p) * a$,为了保证输入与输出的期望一致，我们需要进行代码中$x /= retain_prob$这一步。

传统$Dropout$

对于传统的$Dropout$，在训练的时候，我们不需要进行$x /= retain_prob$的这一步，直接进行神经元$Drop$操作。此时，假设输入$x$的期望是$a$，则此时的输出期望为$(1-p)*a$。我们在测试的时候，整个神经元是保留的，因此输出期望为$a$。为了让输入与输出的期望一致，则在测试的阶段，需要乘以$(1-p)$,使其期望值保持$(1-p)*a$。

传统的dropout和Inverted-dropout虽然在具体实现步骤上有一些不同，但从数学原理上来看，其正则化功能是相同的，那么为什么现在大家都用Inverted-dropout了呢？主要是有两点原因：

测试阶段的模型性能很重要，特别是对于上线的产品，模型已经训练好了，只要执行测试阶段的推断过程，那对于用户来说，推断越快用户体验就越好了，而Inverted-dropout把保持期望一致的关键步骤转移到了训练阶段，节省了测试阶段的步骤，提升了速度。
dropout方法里的 $p$是一个可能需要调节的超参数，用Inverted-dropout的情况下，当你要改变 $p$ 的时候，只需要修改训练阶段的代码，而测试阶段的推断代码没有用到 $p$ ，就不需要修改了，降低了写错代码的概率。

DropConnect

$DropOut$的出发点是直接干掉部分神经元节点，那与神经元节点相连接的是啥？是网络权重呀！我们能不能不干掉神经元，我们把网络权值干掉部分呢？$DropConnect$干掉的就是网络权重。

这里先给出数学定义：

$Training$ $Phase$ :

\mathbf{y}=f((\mathbf{W} \circ \mathbf{M}) \mathbf{x}), \quad M_{i, j} \sim \operatorname{Bernoulli}(p)

$Testing$ $Phase$ : \begin{array}{c}

其中具体的方案图就如下所示：

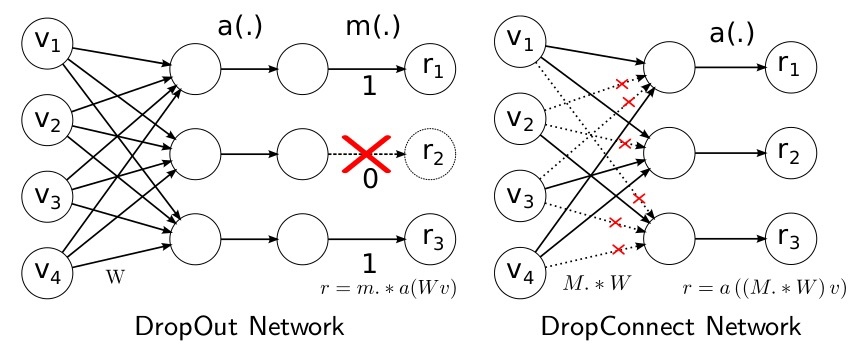
这里给出一个Github上面针对卷积核的2D DropConnect操作。

import torch
import torch.nn as nn
import torch.nn.functional as F
from torch.nn.modules.conv import _ConvNd,_pair

class DropConnectConv2D(_ConvNd):
    def __init__(self, in_channels, out_channels, kernel_size, stride=1,
                 padding=0, dilation=1, groups=1,
                 bias=True, padding_mode='zeros', p=0.5):
        kernel_size = _pair(kernel_size)
        stride = _pair(stride)
        padding = _pair(padding)
        dilation = _pair(dilation)
        super(DropConnectConv2D, self).__init__(
            in_channels, out_channels, kernel_size, stride, padding, dilation,
            False, _pair(0), groups, bias, padding_mode)
        self.dropout = nn.Dropout(p)
        self.p = p

    def _conv_forward(self, input, weight):
        if self.padding_mode != 'zeros':
            return F.conv2d(F.pad(input, self._reversed_padding_repeated_twice, mode=self.padding_mode),
                            weight, self.bias, self.stride,
                            _pair(0), self.dilation, self.groups)
        return F.conv2d(input, weight, self.bias, self.stride,
                        self.padding, self.dilation, self.groups)

    def forward(self, input):
        return self._conv_forward(input, self.dropout(self.weight) * self.p)

if __name__=='__main__':
    conv = DropConnectConv2D(1,1,3,1,bias=False).train()
    conv.weight.data = torch.ones_like(conv.weight)

    a = torch.ones([1,1,3,3])
    print(a)
    print(conv(a))

上面的代码，我们其实只需要主要看下$self.dropout(self.weight) * self.p$这么一部分代码。

如果使用TF的伪代码，也非常好理解了：

def dropconnect(W, p):
    M_vector = tf.multinomial(tf.log([[1-p, p]]), np.prod(W_shape))
    M = tf.reshape(M_vector, W_shape)
    M = tf.cast(M, tf.float32)
    return M * W

$DropConnect$在进行$inference$时，需要对每个权重都进行$sample$，所以$DropConnect$速度会慢些。

在$DropConnect$论文中，作者认为$Dropout$是$2^{|m|}$个模型的平均，而$DropConnect$是$2^{|M|}$个模型的平均（$m$是向量，$M$是矩阵，取模表示矩阵或向量中对应元素的个数），从这点上来说，$DropConnect$模型平均能力更强（因为$|M|$>$|m|$)。当然分析了很多理论，实际上还是$Dropout$使用的更多～。

Spatial Dropout

$Spatial$ $Dropout$目前主要也是分为$1D$, $2D$, $3D$的版本。先看下论文中$Spatial$ $Dropout$的示意图：

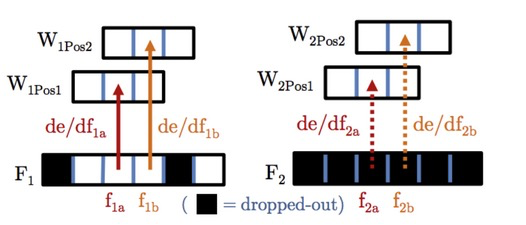
上图左边是传统$Dropout$示意图，右边是$Spatial$ $Dropout$的示意图。

我们以$Spatial$ $Dropout$ $1d$来举例，它是一个文本，其维度($samples$,$sequence_length$,$embedding_dim$)。其中，

$sequence_length$表示句子的长短。
$embedding_dim$表示词向量的纬度。

如下所示：

当使用$dropout$技术时，普通的$dropout$会随机独立地将部分元素置零，而$Spatial$ $Dropout1D$会随机地对某个特定的纬度全部置零。因此$Spatial$ $Dropout$ $1D$需要指定$Dropout$维度，即对应dropout函数中的参数noise_shape。如下图所示：

图中，左边表示的是普通$Dropout$, 右边是$Spatial Dropout 1d$。 $noise_shape$是一个一维张量,就是一个一维数组，长度必须跟$inputs.shape$一样，而且，$noise_shape$的元素，只能是$1$或者$inputs.shape$里面对应的元素。

实际中，哪个轴为$1$，哪个轴就会被一致的$dropout$。因此，从上图中，我们想要实现$Spatial$ $Dropout$ $1D$，$noise_shape$应为($input_shape[0]$, $1$, $input_shape[2]$)

其$Pytorch$代码示意如下：

import torch.nn as nn
from itertools import repeat
class Spatial_Dropout(nn.Module):
   def __init__(self,drop_prob):

       super(Spatial_Dropout,self).__init__()
       self.drop_prob = drop_prob

   def forward(self,inputs):
       output = inputs.clone()
       if not self.training or self.drop_prob == 0:
           return inputs
       else:
           noise = self._make_noise(inputs)
           if self.drop_prob == 1:
               noise.fill_(0)
           else:
               noise.bernoulli_(1 - self.drop_prob).div_(1 - self.drop_prob)
           noise = noise.expand_as(inputs)
           output.mul_(noise)
       return output

   def _make_noise(self,input):
       return input.new().resize_(input.size(0),*repeat(1, input.dim() - 2),input.size(2)) #默认沿着中间所有的shape

目前$Keras$对于$Spatial$ $Dropout$支持的还是不错的，有相对应的$API$接口可以直接用。我们可以使用其$API$进行学习哦～

如$Spatial$ $Dropout$ $1D$的$API$如下所示：

$Spatial$ $Dropout$ $2D$的$API$如下所示:

这里会优先丢弃$channel$层面整个$2D$的特征图，而非如$Dropout$那样的单个元素。

$Spatial$ $Dropout$ $3d$与$2d$比较类似。对于$2d$,丢弃的是$feature$，那么$3d$丢弃的就是$3d$的特征图。

PreviousConv与BN的融合过程 Nextdropout_2

Last updated 2 years ago